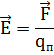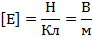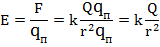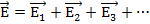Электрическое поле
1. Понятие электрического поля
На уроке о законе Кулона было установлено, что заряженные тела взаимодействуют: одноименно заряженные тела отталкиваются, а разноименно – притягиваются, и, казалось бы, это происходит мгновенно на сколь угодно большом расстоянии, причём пространство между телами ничем не заполнено. В этом состоит теория дальнодействия.
Майклом Фарадеем и Джеймсом Максвеллом была предложена теория близкодействия: вокруг заряженного тела возникает новый, особый вид материи – электрическое поле. Очевидно, что вокруг незаряженных тел электрическое поле отсутствует. Экспериментально было установлено, что электрическое поле может действовать только на электрические заряды и заряженные тела. Таким образом, заряженные тела взаимодействуют посредством электрического поля, в результате чего между ними возникает уже знакомая нам сила электростатического (кулоновского) взаимодействия.
2. Напряженность электрического поля
Определение: Электрическое поле обладает силовой характеристикой. Эта векторная величина называется напряженностью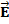 
и определяется для каждой точки пространства вокруг заряженного тела, которое это поле создает.
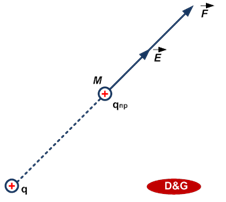
Рассмотрим положительный точечный заряд Q, который, согласно Фарадею и Максвеллу, создаёт вокруг себя электрическое поле. В точку, удаленную на расстояние r от этого заряда поместим пробный заряд qп (тоже положительный). В этом случае на пробный заряд действует сила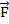 
, как показано на рисунке 1.
Рис. 1. Электростатическое взаимодействие зарядов
Если увеличить величину пробного заряда в два раза, то и значение силы взаимодействия увеличится в два раза. Этот вывод можно сделать из увеличения ускорения в два раза при неизменной массе пробного заряда. Если знак заряда изменить на противоположный, то и направление силы изменится на противоположное. Следовательно, сила взаимодействия прямо пропорциональна величине пробного заряда, а данная точка пространства характеризуется напряженностью электрического поля заряда Q, совпадающего по направлению с силой .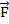
Таким образом, для напряженности можем записать:
|
|
Единица измерения напряженности электрического поля:
|
|
Найдём модуль вектора напряженности электрического поля, которое создается зарядом Q, в точке на расстоянии от него, используя известное из закона Кулона выражение для силы электростатического взаимодействия данного и пробного зарядов:
|
|
Таким образом, величина напряженности электрического поля зависит только от заряда, который это поле создает, и от расстояния между зарядом и точкой, для которой вычисляется значение напряженности. Вектор напряженности лежит на прямой, соединяющий заряд и данную точку, а о направлении этого вектора будет сказано ниже.
3. Суперпозиция электрических полей
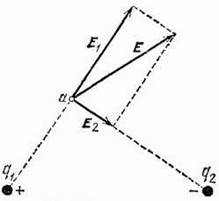
Найдём напряженность электрического поля, которое создается двумя зарядами, пользуясь принципом суперпозиции: каждый заряд создаёт электрическое поле в одной и той же точке так, как будто другого заряда нет (см. рис. 2).
Рис. 2. Напряженность электрического поля двух зарядов.
Заметим, что вектор напряженности электрического поля положительного заряда направлен от него, а отрицательного – к нему. Результирующий вектор напряженности электрического поля двух зарядов в данной точке является геометрической (векторной) суммой векторов напряженностей обоих зарядов и находится по правилу сложения векторов методом параллелограмма. Выражение для полученного таким образом вектора напряженности в случае произвольного количества зарядов записывается так:
|
|
4. Силовые линии электрического поля
Электрическое поле, создаваемое одним или несколькими заряженными телами, можно изобразить графически с помощью силовых линий.
Определение: Силовые линии электрического поля – это непрерывные линии, касательные к которым в каждой точке совпадают по направлению с векторами напряженности (см. рис. 3).
Рис. 3. Силовые линии произвольного электрического поля
Изображение электрического поля с помощью силовых линий очень субъективно, но необходимо придерживаться следующих правил:
силовые линии не пресекаются, то есть через каждую точку пространства может проходить только одна силовая линия;
силовые линии не замкнуты, то есть начинаются на положительных зарядах и заканчиваются на отрицательных;
густота силовых линий определяет, насколько велика абсолютная величина напряженности электрического поля в данной области пространства.
Используя эти правила, рассмотрим для начала силовые линии электрического поля уединенных зарядов – зарядов, которые расположены на огромном расстоянии от других зарядов и не ощущающих влияния с их стороны (см. рис. 4).
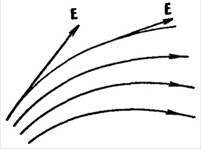
Рис. 4. Силовые линии электрических полей различных уединенных зарядов
Заряд q1 в два раза больше заряда q2 по абсолютной величине, поэтому он создает в два раза более сильное электрическое поле, и, по собственной договоренности, изображаем силовые линии вокруг него в два раза гуще. Силовые линии электрического поля уединенного заряда уходят в бесконечность. Напряженность поля очень сильно уменьшается с увеличением расстояния от заряда. В действительности рассмотреть поле уединенного заряда и зарегистрировать очень маленькое значение напряженности на большом расстоянии от него очень сложно.
Если силовые линии электрического поля параллельны друг другу и их густота одинакова, то такое электрическое поля называется однородным и не изменяется с расстоянием. Если силовые линии не параллельны друг другу и их густота разная в различных областях пространства, то такое поле называется неоднородным. Область пространства, в которой силовые линии гуще, характеризуется бóльшим значением напряженности, чем область пространства, в которой силовые линии реже.
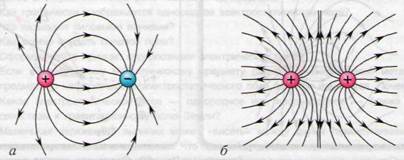
Рассмотрим теперь электрическое поле, созданное двумя разноименными зарядами, одинаковыми по абсолютной величине, разнесенными на конечное расстояние, или электрическим диполем (см. рис. 5а). Электрическое поле двух одинаковых одноименных зарядов изображено на рис. 5б. В небольшой области пространства между зарядами электрическое поле и вовсе отсутствует.
Рис. 5. Силовые линии поля электрического диполя (а) и одноименных зарядов (б)