Графики равномерного прямолинейного движения
Для начала рассмотрим законы равномерного прямолинейного движения, полученные нами ранее:
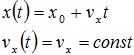
Если внимательно исследовать эти выражения, видно, что обе зависимости являются линейными. Из курса алгебры вы должны знать, что графиком любой линейной зависимости является прямая линия. Поскольку скорость тела при равномерном прямолинейном движении не меняется, графиком этой зависимости всегда будет прямая, параллельная оси времени.
Построим данные зависимости (Рис. 1):
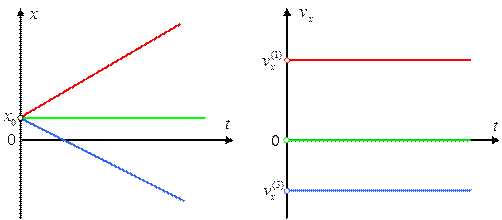
Рис. 1. Графики равномерного прямолинейного движения при разных скоростях
На левом графике изображена зависимость координаты трех разных движущихся тел от времени. Красный график соответствует случаю, когда скорость тела направлена в ту же сторону, что и ось координат. Зеленый график соответствует случаю покоящегося тела. Синий – случаю, когда скорость противоположно направлена к оси координат. Точка  , в которой каждый из трех графиков пересекает ось
, в которой каждый из трех графиков пересекает ось  , – это начальная координата тела.
, – это начальная координата тела.
На правом графике изображены зависимости скоростей тела от времени. Поскольку при равномерном прямолинейном движении скорости тел не меняются, графики являются прямыми, параллельными оси времени. Красный график соответствует положительной скорости (скорость направлена в ту же сторону, что и ось координат), зеленый график соответствует покоящемуся телу (скорость постоянна и равна нулю), а синий – отрицательной скорости (скорость противоположно направлена оси координат).
Таким образом, мы можем восстановить законы движения по графикам:
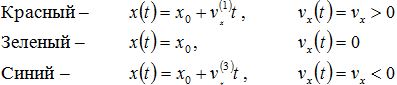
Поговорим о начальной координате. Эту величину всегда можно определить как точку пересечения графика зависимости координаты от времени с осью координат (Рис. 2).
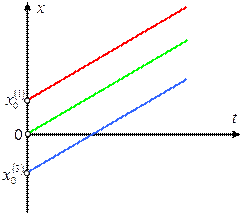
Рис. 2. Графики равномерного прямолинейного движения тел с разными начальными положениями
Из графиков видно, что начальное положение тела, соответствующего красной кривой, положительно, зеленой кривой – равно нулю, а синей – отрицательно.
Обсудим теперь то, как можно получить из графика скорость тела при равномерном прямолинейном движении. Из курса алгебры вы должны знать, что линейная зависимость задается выражением
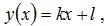
где коэффициент 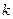 равен тангенсу угла наклона прямой на графике. Эта зависимость аналогична закону движения тела при равномерном прямолинейном движении. Таким образом, скорость – это тангенс угла наклона графика зависимости координаты тела от времени (Рис. 3).
равен тангенсу угла наклона прямой на графике. Эта зависимость аналогична закону движения тела при равномерном прямолинейном движении. Таким образом, скорость – это тангенс угла наклона графика зависимости координаты тела от времени (Рис. 3).
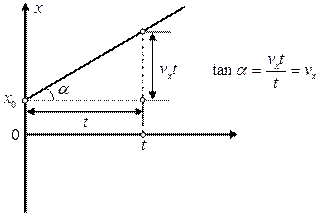
Рис. 3. Связь между тангенсом угла наклона графика координаты от времени и скоростью тела при равномерном прямолинейном движении
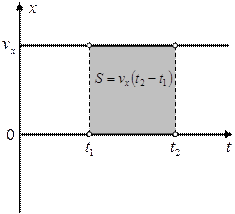
Рис. 4. Связь между путем, пройденным телом, и площадью под графиком зависимости скорости тела от времени
Осталось поговорить о том, как, зная график скорости тела от времени, определить пройденный путь за какой-либо промежуток времени. Оказывается, что путь равен площади фигуры, ограниченной осью времени, прямыми 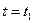 и
и 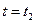 , и графиком зависимости скорости от времени (Рис.4).
, и графиком зависимости скорости от времени (Рис.4).
Итак, мы изучили, как, зная законы движения тел, движущихся равномерно и прямолинейно, нарисовать графики зависимости скорости тела от времени и координаты тела от времени. Корме того, мы научились определять по графикам зависимостей координаты и скорости от времени, определять начальное положение, скорость тела и пройденный телом путь.
