Равномерное прямолинейное движение

Пря­мо­ли­ней­ным рав­но­мер­ным на­зы­ва­ют такое дви­же­ние, при ко­то­ром тело за любые рав­ные про­ме­жут­ки вре­ме­ни со­вер­ша­ет оди­на­ко­вые пе­ре­ме­ще­ния.

А будет ли рав­но­мер­ным пря­мо­ли­ней­ным дви­же­ние, при ко­то­ром тело за каж­дую се­кун­ду про­хо­дит оди­на­ко­вое рас­сто­я­ние, со­вер­шая оди­на­ко­вые пе­ре­ме­ще­ния, на­при­мер один сан­ти­метр? На пер­вый взгляд – да. Но, если тело будет про­хо­дить этот сан­ти­метр за пер­вые пол­се­кун­ды, а вто­рые пол­се­кун­ды будет по­ко­ить­ся, дви­же­ние не будет рав­но­мер­ным: тело пол­се­кун­ды дви­га­лось, а потом по­ко­и­лось. По­это­му в фор­му­ли­ров­ке клю­че­вое слово – «любые», любые рав­ные про­ме­жут­ки вре­ме­ни.

При­ме­ром та­ко­го дви­же­ния могут слу­жить дви­же­ние пу­зырь­ков в воде, па­де­ние ка­пель в воз­ду­хе, дви­же­ние по­ез­да или ав­то­мо­би­ля на от­дель­ных участ­ках пути, дви­же­ние мо­ле­ку­лы газа между столк­но­ве­ни­я­ми с дру­ги­ми мо­ле­ку­ла­ми. В ре­аль­ной жизни мы очень редко стал­ки­ва­ем­ся с рав­но­мер­ным пря­мо­ли­ней­ным дви­же­ни­ем, но оно очень удоб­но, чтобы при по­мо­щи его мо­де­ли­ро­вать дру­гие, более слож­ные, виды дви­же­ния.

По­зна­ко­мим­ся с пер­вой ха­рак­те­ри­сти­кой – ско­рость пря­мо­ли­ней­но­го рав­но­мер­но­го дви­же­ния. При пря­мо­ли­ней­ном рав­но­мер­ном дви­же­нии пе­ре­ме­ще­ние прямо про­пор­ци­о­наль­но вре­ме­ни (рис. 1). 

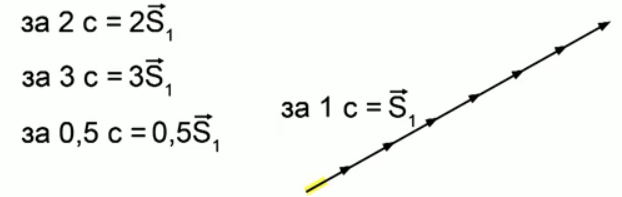
Рис. 1. За­ви­си­мость пе­ре­ме­ще­ния от вре­ме­ни

Мы видим, что от­но­ше­ние пе­ре­ме­ще­ния ко вре­ме­ни для та­ко­го дви­же­ния будет ве­ли­чи­ной по­сто­ян­ной. Это поз­во­ля­ет вве­сти такое от­но­ше­ние в ка­че­стве глав­ной ха­рак­те­ри­сти­ки пря­мо­ли­ней­но­го рав­но­мер­но­го дви­же­ния, ко­то­рую мы на­зы­ва­ем ско­рость рав­но­мер­но­го пря­мо­ли­ней­но­го дви­же­ния.

Ско­ро­стью пря­мо­ли­ней­но­го рав­но­мер­но­го дви­же­ния на­зы­ва­ет­ся от­но­ше­ние пе­ре­ме­ще­ния тела 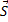 ко вре­ме­ни t:

  = 

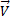Ско­рость – век­тор­ная ве­ли­чи­на. Мо­дуль ско­ро­сти чис­лен­но равен мо­ду­лю пе­ре­ме­ще­ния тела за еди­ни­цу вре­ме­ни, а на­прав­ле­ние ско­ро­сти сов­па­да­ет с на­прав­ле­ни­ем пе­ре­ме­ще­ния.

Зная опре­де­ле­ние ско­ро­сти, мы можем сфор­му­ли­ро­вать, что если тело за любые рав­ные про­ме­жут­ки вре­ме­ни со­вер­ша­ет оди­на­ко­вые пе­ре­ме­ще­ния, то оче­вид­но, что это дви­же­ние с по­сто­ян­ной ско­ро­стью. Пря­мо­ли­ней­ное рав­но­мер­ное дви­же­ние – это дви­же­ние, когда тело дви­жет­ся с по­сто­ян­ной ско­ро­стью не толь­ко по мо­ду­лю, но и по на­прав­ле­нию.

Зная ско­рость рав­но­мер­но­го пря­мо­ли­ней­но­го дви­же­ния, неслож­но опре­де­лить пе­ре­ме­ще­ние, ко­то­рое тело со­вер­ша­ет за любой про­ме­жу­ток вре­ме­ни, то есть неслож­но ре­шить глав­ную за­да­чу ме­ха­ни­ки.

Из опре­де­ле­ния ско­ро­сти сле­ду­ет, что век­тор пе­ре­ме­ще­ния 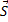 равен про­из­ве­де­нию век­то­ра ско­ро­сти на время  · :  =  · 

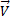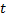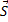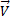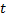
в про­ек­ци­ях на оси ко­ор­ди­нат это будет иметь сле­ду­ю­щий вид:

  =  · ;  =  · ;  =  ·  

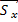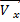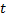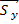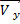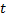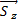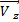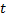
По­сколь­ку ра­ди­ус-век­тор тела в любой мо­мент вре­ме­ни за­да­ет­ся со­от­но­ше­ни­ем

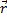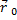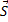 =  + , то по­лу­ча­ем   =  +  · 

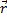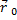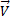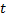
Мы по­лу­чи­ли ре­ше­ние глав­ной за­да­чи ме­ха­ни­ки в век­тор­ной форме. В про­ек­ци­ях на оси ко­ор­ди­нат мы по­лу­чим: x = x₀ + V_x· t

y = y₀ + Vy · t

z = z₀ + Vz · t

Для рав­но­мер­но­го пря­мо­ли­ней­но­го дви­же­ния удоб­нее всего вы­брать одну из осей вдоль тра­ек­то­рии дви­же­ния тела, а тра­ек­то­рия яв­ля­ет­ся пря­мой ли­ни­ей, тогда оче­вид­но, что для опи­са­ния дви­же­ния до­ста­точ­но одной фор­му­лы. На­при­мер, x = x₀+ V_x · t, чаще всего она за­пи­сы­ва­ет­ся x = x₀ + V · t без знач­ка х в про­ек­ции ско­ро­сти. Сле­ду­ет пом­нить, что V – это не мо­дуль ско­ро­сти, а ее про­ек­ция. Раз­ни­ца в том, что мо­дуль не может быть от­ри­ца­тель­ным, а про­ек­ция может. Если рас­смот­реть дви­же­ние ав­то­мо­би­лей, дви­га­ю­щих­ся нав­стре­чу друг другу, то дви­же­ние будет од­но­мер­ным, нам до­ста­точ­но вы­брать одну ось для опи­са­ния этого дви­же­ния. Про­ек­ция ско­ро­сти од­но­го из ав­то­мо­би­лей будет по­ло­жи­тель­ной, а дру­го­го от­ри­ца­тель­ной. Если про­ек­ция ско­ро­сти от­ри­ца­тель­на, зна­чит, тело дви­жет­ся в сто­ро­ну про­ти­во­по­лож­ную вы­бран­ной оси.

 Примеры задач

За­да­ча 1.

Ав­то­мо­биль дви­жет­ся по пря­мо­му шоссе с по­сто­ян­ной ско­ро­стью 72 км/ч. За­пи­ши­те урав­не­ние за­ви­си­мо­сти его ко­ор­ди­на­ты от вре­ме­ни, на­пра­вив ось Ох в сто­ро­ну дви­же­ния, вы­брав на­ча­ло ко­ор­ди­нат у ав­то­за­пра­воч­ной стан­ции, а на­ча­ло от­сче­та вре­ме­ни – в мо­мент, когда ав­то­мо­би­лю оста­лось про­ехать до АЗС еще 500 м (рис. 2, 3).

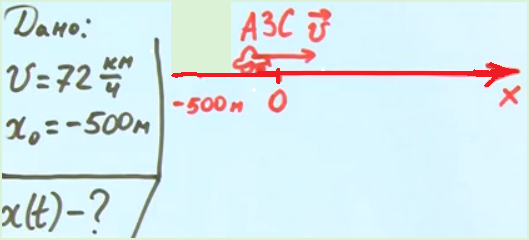
Рис. 2. При­мер за­да­чи 1

Пе­ре­ве­дя ки­ло­мет­ры и часы в метры и се­кун­ды и видя, что на­прав­ле­ние про­ек­ции ско­ро­сти сов­па­да­ет с на­прав­ле­ни­ем оси, мы можем за­пи­сать:

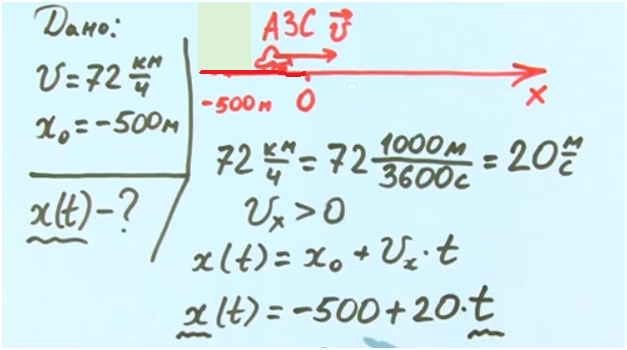
Рис. 3. Ре­ше­ние за­да­чи 1

Мы можем опре­де­лить по­ло­же­ние тела в любой мо­мент вре­ме­ни, под­ста­вив зна­че­ние пе­ре­мен­ной t.

За­да­ча 2.

Опи­ши­те дви­же­ние тела вдоль оси Ох, если за­ви­си­мость ко­ор­ди­на­ты от вре­ме­ни имеет вид: х = -5 + 3t

За­пи­шем тот закон, ко­то­рый нам дан в усло­вии за­да­чи: х(t) = -5 + 3t

Нам необ­хо­ди­мо опи­сать дви­же­ние тела. Это зна­чит опи­сать:

Как дви­га­лось тело.

За­пи­сать ха­рак­те­ри­сти­ки дви­же­ния.

Из усло­вия за­да­чи, мы видим, что:

Тело дви­га­лось рав­но­мер­но пря­мо­ли­ней­но х(t) = х₀ + V_xt

На­чаль­ная ко­ор­ди­на­та тела х₀ = -5 м; мо­дуль ско­ро­сти V = 3 м/c и сов­па­да­ет с на­прав­ле­ни­ем оси, то есть по­ло­жи­тель­но V_x › 0

х₀ = -5 м; V = 3 м/c; V_x › 0

Мы с вами пол­но­стью опи­са­ли дан­ное дви­же­ние, за­да­ча ре­ше­на.