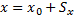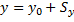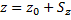Пространство и время. Координаты. Вектор перемещения. Радиус-вектор
Пространство и время. Координаты
Все события в нашей жизни происходят в пространстве и с течением времени, поэтому необходимо научиться описывать пространство и время, то есть отвечать на вопросы «где?» и «когда?».
Для того чтобы ответить на вопрос «где?», учёные ввели термин «система координат», то есть какие-то независимые переменные, которые однозначно задают положение тела.
Наше пространство трёхмерное, то есть через любую точку можно провести три взаимно перпендикулярные прямые. Это лёгло в основу самой распространённой системы координат – прямоугольной (декартовой).
Можно выбрать три взаимно перпендикулярных оси (декартова система координат), связав начало координат с телом отсчёта. В такой системе отсчёта положение точки (M) будут характеризовать три числа, которые называются декартовыми координатами. Для их нахождения необходимо опустить перпендикуляры из точки на три оси (OX, OY, OZ) (см. Рис. 1).
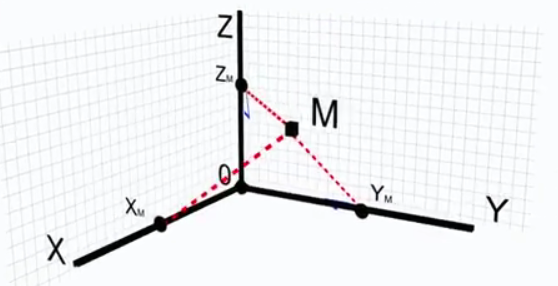
Рис. 1. Определение координат точки
Координаты также можно определить, если опустить из точки M на плоскость XOY перпендикуляр, а затем из точки 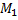 провести перпендикуляр к оси OX, таким образом, получаем координату x(см. Рис. 2). Аналогично находим две другие координаты точки.
провести перпендикуляр к оси OX, таким образом, получаем координату x(см. Рис. 2). Аналогично находим две другие координаты точки.
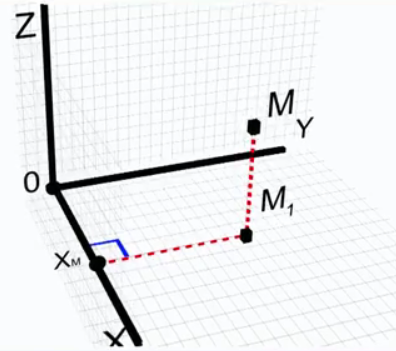
Рис. 2. Определение координаты точки
В физике, в математике и в повседневной жизни используются также и другие системы координат. Например, для определения местоположения на глобусе (земном шаре) используются географические координаты (широта и долгота), которые являются производной от сферической системы координат. В некоторых задачах по физике и математике удобно использовать цилиндрические системы координат.
Для того чтобы ответить на вопрос «когда?», то есть охарактеризовать время события, необходимо задать одну независимую величину – временную координату. Её мы используем, когда говорим, что какое-либо событие произошло в 1861 году или, например, что спортсмен пробежал дистанцию за 10 секунд (в качестве начала отсчёта выбираем стартовый сигнал пистолета).
Следовательно, для полного ответа на вопрос «где?» и «когда?» необходимо задать четыре независимые величины – координаты x, y, z и t(время).
Можно обойтись и меньшим количеством переменных. Если рассматривать плоское движение тела, например движение водомерки по поверхности воды, то удобно выбрать оси OXи OY именно в этой плоскости, а ось OZ перпендикулярно ей (см. Рис. 3). Эта ось не пригодится, так как координата z будет равна нулю. Такое движение называется двумерным. Если тело движется вдоль одной прямой, то достаточно только координаты x для описания изменения его положения в пространстве с течением времени (движение автомобиля по прямой дороге) – одномерное движение.
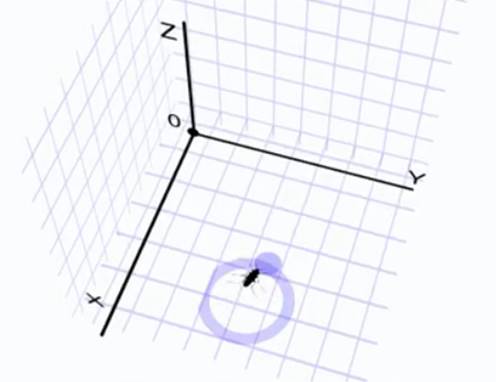
Рис. 3. Двумерное движение
Следовательно, если найти зависимости координат от времени, то есть законы 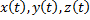 , то можно решить главную задачу механики – определить положение тела (координату) в любой момент времени.
, то можно решить главную задачу механики – определить положение тела (координату) в любой момент времени.
Вектор перемещения
Зная координаты и путь, не всегда можно определить местоположение тела через некоторое время. Для этого необходимо знать длину и направление отрезка, соединяющего начальное положение тела с последующим. Такой направленный отрезок называют перемещением (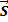 ) (см. Рис. 4).
) (см. Рис. 4).
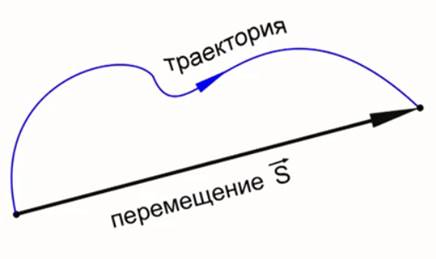
Рис. 4. Вектор перемещения
Перемещением тела (материальной точки) называют вектор, проведённый из начального положения тела в его положение в данный момент времени. Длину направленного отрезка S называют модулем перемещения.
Радиус-вектор
В физике также пользуются радиус-вектором, который характеризует положение тела и удобен для описания движения тела.
Радиус-вектор (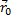 ) материальной точки проводят из начала координат к положению точки в данный момент (см. Рис. 5). При движении точки радиус-вектор изменяется, и в определённый момент времени он будет равен:
) материальной точки проводят из начала координат к положению точки в данный момент (см. Рис. 5). При движении точки радиус-вектор изменяется, и в определённый момент времени он будет равен:
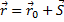 ,
,
где 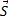 – вектор перемещения;
– вектор перемещения; 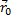 – радиус-вектор в начальный момент времени.
– радиус-вектор в начальный момент времени.
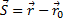
Из рисунка 5 видно, что проекции радиус-вектора на оси координат равны координатам материальной точки.
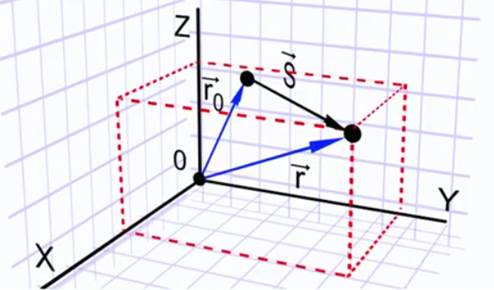
Рис. 5. Радиус-вектор материальной точки
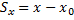
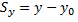
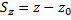
То есть, проекция вектора перемещения на ось координат равна изменению соответствующей координаты тела. Следовательно, конечные координаты тела будут равны: