Решение задач повышенной сложности на движение в НСО
Пример задачи
Найти вес тела на широте φ (рис. 1).
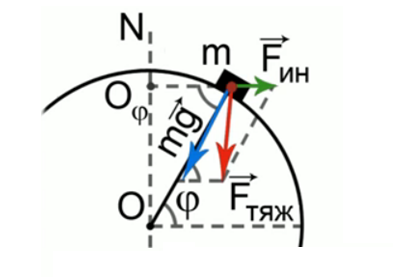
Рис. 1. Пример решения задачи
Pφ – ? 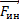 = -m
= -m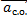 ;
; 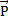 =
= 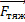 = m
= m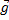 +
+ 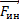
ac.o. = aц.с. = 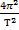 Rзcosφ
Rзcosφ
Fтяж = 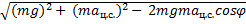
Fтяж = m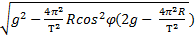 ;
; 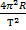 = aэ = 0,03385 м/с2
= aэ = 0,03385 м/с2
Fтяж = m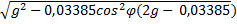
Мы привыкли, что вес тела – mg, но Земля совершает свое движение вокруг своей оси и является неинерциальной системой отсчета.
Рассмотрим тело, которое находится на поверхности Земли на широте φ. Широта определяется направлением на эту точку земной поверхности, и угол, который она составляет с экваториальной плоскостью, как раз и является широтой места.
На тело в неинерциальной системе отсчета кроме силы гравитационного притяжения 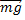 действует еще сила инерции
действует еще сила инерции 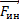 , которая направлена в сторону, противоположную ускорению системы отсчета, и численно равна произведению массы на ускорение этой системы отсчета. А ускорение системы отсчета – ускорение против земной поверхности на широте φ, тогда сила тяжести, которая и равна весу тела, равна сумме этих двух сил. Это векторная сумма и сила тяжести направлена не к центру Земли, а немножко мимо центра. Ускорение против земной поверхности на широте φ составляет отношение 4π2 на период обращения Земли вокруг оси в квадрате, умноженное на радиус окружности, которую описывает данная точка. В данном случае центром окружности является Оφ и радиус окружности – это радиус Земли, умноженный на косинус широты места, тогда по теореме косинусов находим силу тяжести как сторону треугольника, у которого известны две другие стороны и угол между ними.
, которая направлена в сторону, противоположную ускорению системы отсчета, и численно равна произведению массы на ускорение этой системы отсчета. А ускорение системы отсчета – ускорение против земной поверхности на широте φ, тогда сила тяжести, которая и равна весу тела, равна сумме этих двух сил. Это векторная сумма и сила тяжести направлена не к центру Земли, а немножко мимо центра. Ускорение против земной поверхности на широте φ составляет отношение 4π2 на период обращения Земли вокруг оси в квадрате, умноженное на радиус окружности, которую описывает данная точка. В данном случае центром окружности является Оφ и радиус окружности – это радиус Земли, умноженный на косинус широты места, тогда по теореме косинусов находим силу тяжести как сторону треугольника, у которого известны две другие стороны и угол между ними.
Подставляя выражение для центростремительного ускорения, получаем силу тяжести, в формуле которой мы видим ускорение точек земной поверхности на экваторе – аэ. При вычислении получим аэ = 0,03385 м/с2, и, подставляя в выражение для силы тяжести, мы можем определить ее в любой точке поверхности для необходимых широты и массы тел.
Для контроля найдем силу тяжести тела массой 10 кг на экваторе, на широте 600 и на полюсе, сравним полученные значения.

Ответ: при φ = 00Fтяж1 = 94,62 (H),
φ =600 Fтяж2 = 96,33 (H),
φ = 900Fтяж3 = 98 (H).
Естественно, самое маленькое значение будет на экваторе, самое большое – на полюсе.
Задача 1
Грузы массой 2 кг и 8 кг подвешены к концам нити, перекинутой через блок, который поднимается вертикально с ускорением 5 м/с2. Найти силу натяжения нити.
Сложности при решении этой задачи связаны с тем, что ранее говорилось о применении законов Ньютона только в инерциальных системах отсчета и рассматривалось движение этих грузов относительно Земли. Относительно Земли ускорение грузов разное, поэтому задача и стала для многих сложной.
Решать такие задачи необходимо в системе отсчета «Блок» (рис. 2), которая является неинерциальной, и в этой системе отсчета ко всем силам, которые обычно приложены к телам, добавляется сила инерции.
К примеру, когда автобус резко тормозит, нас толкает вниз сила инерции. Здесь при движении блока наверх к каждому из тел добавляется сила, противоположная ускорению блока и направленная вниз.
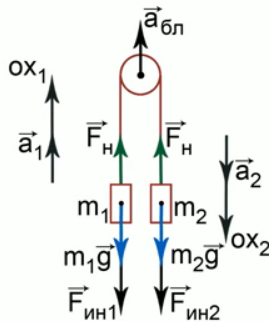
Рис. 2. Система отсчета «Блок»
Эйнштейн доказал, что эта сила инерции в принципе неотличима от силы гравитационного притяжения. В данном случае на первое тело действует сила натяжения нити 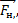 направленная вверх, сила гравитационного притяжения m1
направленная вверх, сила гравитационного притяжения m1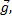 направленная вниз, и сила инерции
направленная вниз, и сила инерции 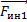 . На второе тело точно так же действует
. На второе тело точно так же действует 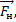 направленная вверх, сила гравитационного притяжения m2
направленная вверх, сила гравитационного притяжения m2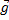 и сила инерции
и сила инерции 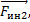 направленные вниз.
направленные вниз.
У нас система связанных тел, для каждого из тел ось необходимо направить в свою сторону по ускорению. Очевидно, что первое тело, которое легче, будет двигаться относительно блока вверх, а второе тело будет двигаться вниз. Поэтому ось ох1направляем вверх, ох2 направляем вниз.
Запишем краткое условие задачи и решение.

Ответ: Fн = 48 H.
Уравнение в проекции на ось ох1 будет иметь вид -m1g - m1абл + Fн = m1а.
На ось ох2 будет m2g + m2абл - Fн = m2а.
Решение системы уравнений достигается сложением, при сложении сразу убираем противоположные значения силы натяжения и получаем выражение, из которого можем записать ускорение и вычислить его. Далее его значение можно подставить в любое из уравнений и определить силу натяжения.
Задача 2
На наклонной поверхности клина с углом 300 покоится брусок при коэффициенте трения 0,69. С каким минимальным ускорением нужно перемещать по горизонтали клин, чтобы брусок стал скользить вниз по его поверхности?
Выполняем краткое условие задачи, рисунок и решение (рис. 3).
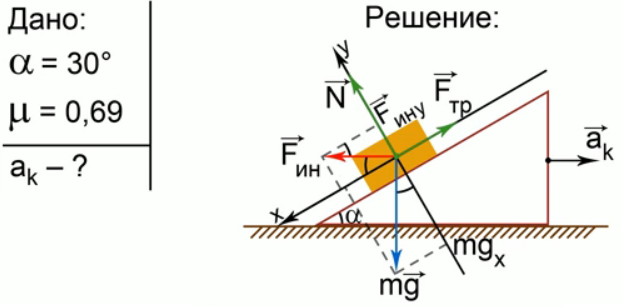
Рис. 3. Решение задачи 2
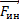 = - m
= - m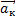 ; m
; m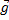 +
+ 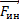 +
+ 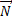 +
+ 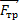 = m
= m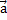 ; a ≥ 0
; a ≥ 0
по ох: mgsinα + maкcosα - Fтр ≥ 0
по оу: -mgcosα + maкsinα + N = 0
N = mgcosα - maкsinα Fтр = μN = μmgcosα - μmaкsinα
mgsinα + maкcosα - μmgcosα + μmaкsinα ≥ 0
aк ≥ 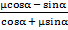 g aк ≥
g aк ≥ 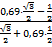 · 10 aк ≥ 0,8 (м/с2)
· 10 aк ≥ 0,8 (м/с2)
Ответ: aк ≥ 0,8 м/с2.
Сила, которая заставляет брусок проскальзывать, – это mgsinα, но sinα = 0,5 при μ = 0,69, мы видим, что сила трения больше силы, составляющей mg. Решаем задачу в системе отсчета «Клин». К тем силам, которые обычно приложены к бруску, – сила реакции опоры 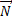 ,
, 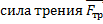 и сила тяжести m
и сила тяжести m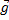 – добавляется сила инерции
– добавляется сила инерции 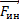 , направленная против ускорения клина. Запишем второй закон Ньютона для бруска и выберем оси, ось х в сторону возможного направления и ось у перпендикулярно поверхности клина. Получаем: по оси х mg проецируется через sinα, это противолежащий катет, сила инерции проецируется через cosα и минус сила трения, так как она направлена в противоположную сторону, будет больше или равно нулю. Когда ускорение равно нулю, то сила инерции принимает минимальное значение, соответственно, ускорение клина тоже минимально.
, направленная против ускорения клина. Запишем второй закон Ньютона для бруска и выберем оси, ось х в сторону возможного направления и ось у перпендикулярно поверхности клина. Получаем: по оси х mg проецируется через sinα, это противолежащий катет, сила инерции проецируется через cosα и минус сила трения, так как она направлена в противоположную сторону, будет больше или равно нулю. Когда ускорение равно нулю, то сила инерции принимает минимальное значение, соответственно, ускорение клина тоже минимально.
По оси у mg будет со знаком минус, так как она направлена против оси у. Уравнение по оси у необходимо, чтобы выразить силу реакции опоры 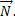 Подставляя значения силы реакции опоры и силы трения, мы получим уравнение, из которого и находим выражение для ускорения клина. Подставляя значения, мы видим, что ускорение, с которым нужно двигать клин в горизонтальном направлении, будет больше или равным 0,8 м/с2.
Подставляя значения силы реакции опоры и силы трения, мы получим уравнение, из которого и находим выражение для ускорения клина. Подставляя значения, мы видим, что ускорение, с которым нужно двигать клин в горизонтальном направлении, будет больше или равным 0,8 м/с2.
При нахождении максимального ускорения его необходимо направить в противоположную сторону.
Задача 3
В центре круглого стола поместили маленькое блюдечко. Коэффициент трения между ним и столом μ = 0,155. Стол двигали прямолинейно с ускорением 2 м/ с2 в течение 2 с, а затем остановили с тем же по величине ускорением. При каком минимальном радиусе стола блюдечко с него не упадет?
Запишем краткое условие задачи, схему и решение (рис. 4).
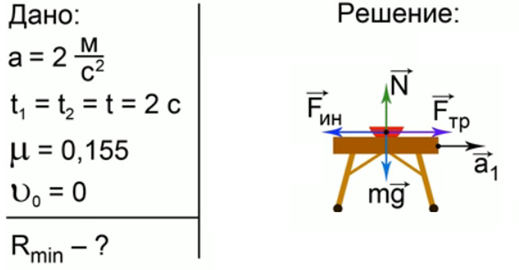
Рис. 4. Решение задачи 3
Fин = ma = 2m; Fтр = μmg = 1,55m
1. t = t1
a1 = 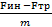 =
= 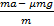
a1 = a - μg V1 = ( a - μg ) t S1 = 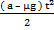
2. t = t2
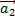 = -
= - 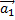 => Fин ↑↑ Fтрa2 = -(a + μg)
=> Fин ↑↑ Fтрa2 = -(a + μg)
V02 = V1 V2 = 0
S2 = 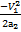 =
= 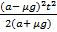 ; S = S1 + S2; S =
; S = S1 + S2; S = 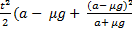 )
)
S = 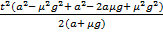 =
= 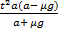 =
= 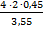 = 1,01 (м)
= 1,01 (м)
Ответ: Rmin = 1,01 м.
Начальная скорость блюдечка равна нулю, оно лежит в центре стола. Когда стол начинает двигаться с ускорением, он становится неинерциальной системой отсчета и ко всем силам, которые были приложены к блюдечку, добавляется сила инерции, направленная против ускорения стола и равная по величине произведению массы на ускорение блюдечка. Сила трения сразу будет мешать блюдечку двигаться. При подстановке известных величин мы видим, что сила трения меньше силы инерции, блюдечко начинает двигаться по поверхности стола.
Первое условие задачи – стол движется с ускорением, в этом случае сила инерции направлена в противоположную сторону силы трения, но больше нее. Определим ускорение, с которым движется блюдечко, по второму закону Ньютона. За это время скорость блюдечка увеличивается с этим ускорением и достигает значения V1, а путь – S1.
При втором промежутке времени ускорение стола меняется на противоположное, соответственно, и сила инерции принимает противоположное направление, в данном случае она будет совпадать с силой трения, то есть и сила инерции, и сила трения тормозят движение блюдечка. Начальная скорость к моменту торможения будет равна V1, а конечная скорость в результате торможения будет равна нулю. Поэтому за время торможения блюдечко пройдет путь S2, так как ускорение у нас отрицательное, то знак минус уйдет из выражения.
Общий путь, который пройдет блюдечко, составляет сумму двух полученных выражений S1 и S2. Проведя алгебраические преобразования и подставляя числовые значения, мы получим, что блюдечко пройдет путь 1,01 метра, то есть радиус стола от центра до края должен быть не меньше этого значения, иначе блюдечко соскользнет.
Заключение
Как мы увидели на примерах решения задач, при учете сил инерции второй закон Ньютона будет справедлив для любой системы отсчета и ряд задач лучше решается в неинерциальной системе отсчета.
