Уравнения кинематики прямолинейного движения тела с ускорением свободного падения
Уравнения кинематики прямолинейного движения тела с ускорением свободного падения
Рассмотрим рисунок такого движения (рис. 1).
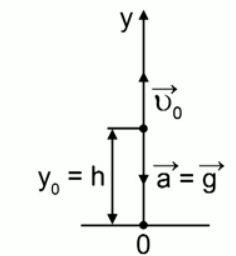
Рис. 1. Прямолинейное движение тела с ускорением свободного падения
Движение происходит по вертикали – по оси у с некоторой точки, расположенной на высоте h.
Начальная скорость V0 направлена вверх, ускорение равно ускорению свободного падения и направлено вниз. Тогда уравнение кинематики, с учетом того, что ау = -g и направлено против координатной оси, принимает вид:
для скорости V(t) = V0 - gt (1);
для координаты тела с учетом того, что у0 = h у = h + V0t - 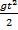 (2);
(2);
время движения тела до верхней точки t↑ = 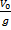 (3);
(3);
время движения тела до падения на землю является корнем квадратного уравнения (2), учитываем то, что время отрицательным быть не может:
tп = 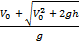 (4)
(4)
скорость момента падения находится по формуле Vп = 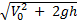 (5);
(5);
максимальная высота траектории тела H = h + 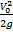 (6).
(6).
Эти шесть формул определяют решение всех задач, которые рассматриваются по этой теме.
Задача 1
Тело, падающее без начальной скорости с некоторой высоты, прошло последние 300 м за 5 с. Найти время падения тела.
Запишем краткое условие задачи, рисунок и решение (рис. 2).
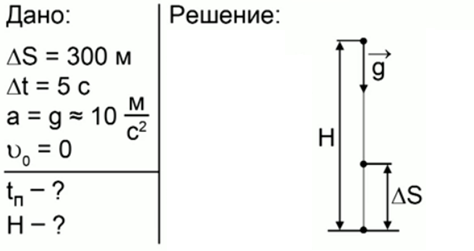
Рис. 2. Решение задачи 1
H = 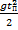 ; H - ΔS =
; H - ΔS = 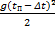
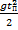 - ΔS =
- ΔS = 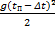 ;
; 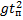 - 2ΔS =
- 2ΔS = 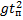 - 2
- 2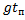 Δt + gΔt2
Δt + gΔt2
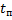 =
= 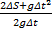 =
= 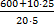 = 8,5 (c) H = 5·8,52 ≈ 361 (м)
= 8,5 (c) H = 5·8,52 ≈ 361 (м)
Ответ: 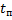 = 8,5 с; Н = 361 м.
= 8,5 с; Н = 361 м.
Нам необходимо найти время падения и высоту, с которой упало тело. Нам известно, что последние 300 м – ΔS – тело прошло за 5 с – Δt, ускорение равно ускорению свободного падения, и в таких задачах оно принимается равным 10 м/с2. Начальная скорость равна нулю, так как тело свободно падающее.
Записываем уравнение кинематики от начальной точки: начальная скорость равна нулю и весь путь будет равен высоте H.
Второе уравнение записываем как участок, предшествующий пути ΔS, учитывая и время падения.
Мы видим, что у нас получилась система уравнений с двумя неизвестными H и tп. Воспользуемся первым уравнением для подстановки H во втором уравнении, тогда во втором уравнении неизвестным будет только tп, которое мы после алгебраических преобразований и определим. Далее, подставляя время падения в исходную формулу, находим высоту, с которой падало тело. Задача решена.
Задача 2
Аэростат равномерно поднимается со скоростью 4 м/с. На высоте 40 м от земли из него бросили вверх предмет со скоростью 6 м/с относительно аэростата. Через сколько времени предмет упадет на землю?
Запишем краткое условие задачи, схему и решение (рис. 3).
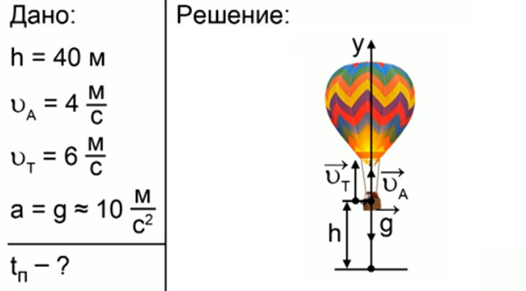
Рис. 3. Решение задачи 2
у = h + V0tп - 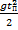 = 0
= 0
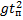 - 2 V0tп - 2h = 0
- 2 V0tп - 2h = 0 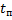 =
= 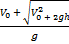 =
= 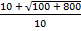 = 4 (c)
= 4 (c)
Ответ: 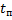 = 4 с.
= 4 с.
Необходимо найти время падения предмета, брошенного с высоты 40 м, причем аэростат движется вверх со скоростью VА = 4 м/с, тело бросили с аэростата со скоростью Vт = 6 м/с,
ускорение равно ускорению свободного падения. Для решения задачи используем уравнение кинематики, но для начала определим скорость V0 относительно земли, которую приобрело тело, для этого складываем скорости аэростата и тела. Далее записываем уравнение для координаты у, ускорение свободного падения у нас будет со знаком минус, так как движение направлено против оси у. Из уравнения находим время падения, произведя алгебраические преобразования и подставляя данные, вычисляем и получаем ответ: предмет упадет на землю через 4 секунды.
{GENERICO:type=adsshortcode}
Задача 3
Ученик, проведя эксперимент по определению ускорения свободного падения, записал результат в виде g = (10,2 ± 0,6) м/с2. Это означает:
1. при проведении эксперимента допущены ошибки;
2. истинное значение g либо 9,6 м/с2, либо 10,8 м/с2;
3. измерить ускорение свободного падения невозможно в таком эксперименте;
4. истинное значение ускорения свободного падения g 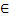 [9,6; 10,8] м/с2.
[9,6; 10,8] м/с2.
Мы видим, что ученик получил результат и погрешность, которую он вычислил, то есть результат может быть больше на 0,6 или меньше. Это верный результат, потому что g лежит в интервале от 9,6 до 10,8 м/с2, истинное значение g = 9,8 м/с2 попало в этот результат, поэтому можно сказать, что лабораторная работа имеет большую погрешность при получении измерений и правильный ответ – 4.
Задача 4
Два тела, свободно падающие с разных высот, достигают земли одновременно. Время падения первого тела – 3 с, а второго – 1 с. На какой высоте было первое тело, когда второе начало падать?
Выполним краткую запись условия задачи, схему и решение (рис. 4).
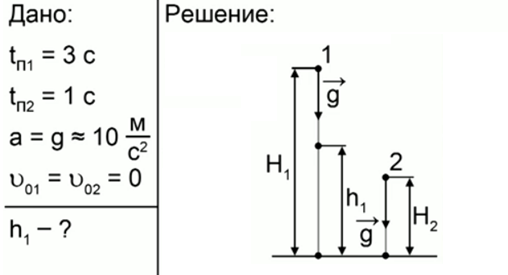
Рис. 4. Решение задачи 4
1. h1 = ΔS3 = 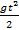 · (2·3 – 1) = 25 (м)
· (2·3 – 1) = 25 (м)
2. H1 = 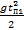 = 5·9 = 45 (м)
= 5·9 = 45 (м)
S1 за 2с = 5·4 = 20 (м)
h1 = 45 – 20 = 25 (м)
Ответ: h1 = 25 м.
Нам необходимо найти h1, начальных скоростей тела не имеют. Тела упали одновременно, но первое тело находилось по времени в полете 2 секунды, когда начало падать второе тело. Решить задачу можно двумя способами.
1. Для первого тела искомая высота h1 – это путь, который прошло свободно падающее тело за третью секунду от начала падения. Две секунды оно падало в одиночестве, а потом начало падать второе тело, в третью секунду они падают параллельно и одновременно ударяются о землю. Тогда можно применить формулу пути, пройденного за третью секунду от начала движения ΔS3, и, подставляя данные, получить результат 25 метров.
2. Тело падало с высоты H1, подставляя в формулу данные, найдем ее. Предыдущий путь S1 за 2 с тело прошло за две секунды, и по этой же формуле найдем путь, который прошло тело за первые две секунды. Произведя вычитание, получим необходимую нам высоту.
Заключение
При решении задач необходимо помнить, что все заданные величины нужно привести к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы:
расстояние S измеряется в м, время t – в с, скорость V – в м/с.
