Неинерциональные системы отсчёта. Силы инерции
Введение
Все законы природы, законы Ньютона, законы сохранения и изменения различных физических величин, которые были изучены ранее, выполняются в инерциальных системах отсчёта. Однако инерциальные системы отсчёта – это идеализация. Любое тело, с которым мы свяжем систему отсчёта, будет подвержено воздействию различных окружающих тел и относительно идеальной инерциальной системы отсчёта будет двигаться с ускорением. Следовательно, любая реальная система отсчёта является неинерциальной.
На этом уроке мы рассмотрим, как меняются законы природы, если попытаться их сформулировать в неинерциальных системах отсчёта.
Основные сведения о неинерциальных системах отсчёта
Дана некоторая гипотетическая инерциальная система отсчёта, в которой выполняются законы Ньютона. Рассмотрим поведение тела массой M (с которым в дальнейшем свяжется неинерциальная система отсчёта) в данной идеальной системе отсчёта. На это тело действуют различные силы F, сумма которых приводит к ускорению (A) тела: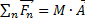 
.
Любое другое тело в этой системе отсчёта, например, с массой m будет подвержено внешним воздействиям, которые измеряются силами f и сумма этих сил (по второму закону Ньютона) равна массе, умноженной на ускорение aэтого тела: 
.
Рассмотрим неинерциальную систему отсчёта, связанную с телом массой M. Законы динамики можно применять и в таких системах. Необходимо произвести тождественные преобразования над законами Ньютона. От обеих частей равенства 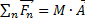отнимем 
: 
.
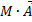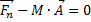От обеих частей равенства отнимем 
: 
.
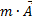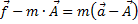В системе отсчёта, связанной с телом, которое движется с ускорением 
, тело массой m будет иметь ускорение 
. Следовательно, можно сказать, что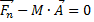 
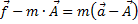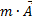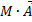– это уравнение движения для покоящегося тела, а – это второй закон Ньютона для тела, которое движется с ускорением . Видно, что в левых частях этих равенств находятся некоторые добавки ( и ), которые называются силами инерции.
Силы инерции – фиктивные силы, которые проявляют себя в неинерциальных системах отсчёта как силы, приводящие к изменению состояния тела, то есть к его ускорению.
Таким образом, второй закон Ньютона может быть записан в любой неинерциальной системе отсчёта, если каждому телу с массой m добавить силу, которая на него действует, и величина этой силы будет равна минус его масса умножить на ускорение выбранной системы отсчёта относительно произвольной инерциальной системы отсчёта: 
.
Наблюдатель, находящийся в автомобиле, который разгоняется или тормозит с некоторым ускорением, испытывает действие силы, прижимающей его к сиденью или выталкивающей из сиденья. Это и есть проявление фиктивных сил инерции, которые появляются в неинерциальной системе отсчёта в данном случае в системе отсчёта, связанной с ускоренно движущимся автомобилем.
Решение задач с помощью неинерциальных систем отсчёта
Задача 1
На некоторой платформе расположено тело (кубик). Между телом и поверхностью платформы существует трение. При движении платформы (направо) с ускорением a тело может соскальзывать с платформы или переворачиваться (см. рис. 1). Необходимо определить, что будет с телом при ускоренном движении платформы.
Рис. 1. Иллюстрация к задаче
Решение
1) Рассмотрим силы, действующие на кубик при ускоренном движении платформы (см. рис. 2):
- сила тяжести величиной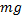 
, приложенная к центру тяжести этого кубика;
- сила реакции опоры со стороны платформы, направленная вертикально вверх и равная N (точка приложения этой силы находится где-то на нижней части кубика);
- сила трения, возможно направленная направо и приложенная где-то в нижней части кубика, равная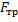 
.
2) Рассмотрим движение кубика на платформе, перейдя в неинерциальную систему отсчёта, связанную с платформой. На кубик в этой системе отсчёта будет действовать сила инерции, равная по величине массе, умноженной на ускорение системы отсчёта, и направленная в противоположную, по отношению к ускорению, сторону (см. рис. 2). В этой неинерциальной системе отсчёта кубик покоится (не двигается, не переворачивается), это означает, что сумма сил, действующих на этот кубик, должна быть равна нулю. Кроме того, так как кубик не переворачивается, то сумма моментов сил, действующих на этот кубик относительно любой точки, должна быть равна нулю.
3) Используя данные условия, вычислим значения параметров задачи, при которых кубик начнёт соскальзывать или переворачиваться.
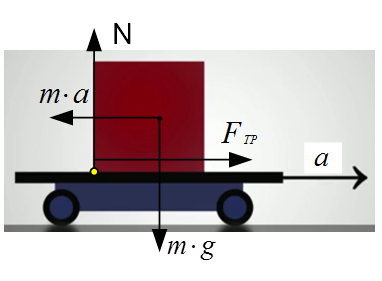
Рис. 2. Силы, действующие на кубик
а) Если кубик не соскальзывает с платформы, то сумма сил, действующих на него в горизонтальном направлении, равна нулю, то есть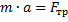 
, где 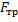, в данном случае, это сила трения покоя.
Следовательно, предположение о том, что 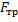направлена направо, верное.
б) Если кубик не переворачивается, то моменты всех сил относительно возможной точки переворота равны нулю. На рис. 2 показано, где находится возможная точка переворота (выделена жёлтым цветом), следовательно, момент силы реакции опоры, момент силы инерции и момент силы тяжести относительно этой точки в сумме должны давать ноль.
в) Если кубик начинает соскальзывать, то 
становится больше силы трения покоя, то есть силы трения скольжения, которая равна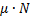 
: 
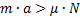. Так как 
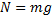, то 
.
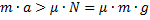Следовательно, получили из неравенства условие. Кубик начнёт соскальзывать, если ускорение станет больше, чем коэффициент трения, умноженный на ускорение свободного падения: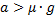 
.
г) Если начинается переворот кубика, то сила реакции опоры приложена в той точке, которая опирается на опору (выделена жёлтым цветом). Момент данной силы относительно этой точки равен нулю. Из-за того что кубик имеет определённую форму, плечи сил и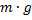 
будут одинаковыми, поэтому моменты сил, равные величинам сил, умноженные на плечо, сводятся к самим силам. Следовательно, условия начала переворота: 
. 
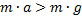Ответ
Если коэффициент трения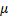 
будет меньше 1, то кубик начнёт скользить. Если коэффициент трения больше 1, то кубик начнёт переворачиваться.
Такое решение задачи в инерциальной системе отсчёта невозможно, так как в такой системе кубик и платформа движутся ускоренно, и использовать условия статического равновесия твёрдого тела, движущегося при этом ускоренно, невозможно.
Задача 2
Мотоциклист едет по дороге, которая представляет собой дугу (см. рис. 3) окружности радиусом R. При этом скорость мотоциклиста равна V. Зачем и на какой угол (
) должен наклониться мотоциклист при таком повороте?
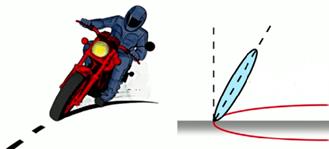
Рис. 3. Иллюстрация к задаче
Решение
1) По законам кинематики, мотоциклист движется с ускорением a (центростремительное ускорение), направленным к центру окружности и равным: 
.
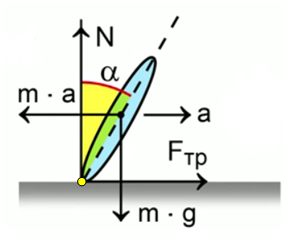
Рис. 4. Силы, действующие на мотоциклиста
2) В процессе такого движения на мотоциклиста действуют (см. рис. 4):
-сила тяжести (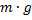), направленная вертикально вниз;
-сила трения (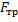), приложенная в точке опоры колеса о поверхность дороги (выделенная жёлтым) и направленная, возможно, к центру окружности, по которой движется мотоциклист;
- сила реакции опоры (N), приложенная в точке опоры колеса о поверхность дороги и направленная вертикально вверх.
3) Если центр масс мотоциклиста находится на одном и том же уровне, то сумма сил по вертикале равна нулю.
4) Сумма сил по горизонтали в инерциальной системе отсчёта должна быть направлена к центру окружности и равна массе, умноженной на ускорение (). Кроме силы трения, никакая другая сила не может быть направлена в центр окружности, следовательно: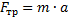 
.
5) Перпендикулярно направлению движения мотоциклиста может быть направлена только сила трения покоя между поверхностью колеса и поверхностью дороги. Если бы колесо скользило относительно поверхности дороги, то сила трения была бы силой трения скольжения. Тогда она была бы направлена против направления движения мотоцикла и мотоциклист не смог бы поворачивать по дуге окружности радиусом R. Следовательно,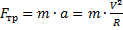 
.
Эта сила не должна превышать силы трения скольжения: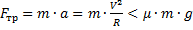 
.
6) При каком условии мотоциклист не будет переворачиваться, узнать в инерциальной системе отсчёта невозможно, так как сумма моментов сил, действующих на мотоциклиста относительно точки опоры, не равна нулю. Это означает, что мотоциклист всё время падает, но чтобы не упасть, мотоцикл поворачивает. То есть происходит очень сложное движение, динамика которого требует очень сложных математических расчётов. При переходе в неинерциальную систему отсчёта мотоциклист оказывается в покое.
7) Кроме перечисленных ранее сил, в неинерциальной системе отсчёта на мотоциклиста действует сила инерции () (см. рис. 4), направленная против направления ускорения и равная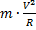 
. Сумма моментов всех сил, действующих на мотоциклиста относительно любой точки, должна быть равна нулю.
Рассмотрим моменты сил относительно точки опоры:
- 
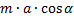– момент силы инерции
- 
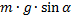– момент силы тяжести
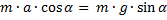
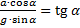
Ответ
Следовательно, движение возможно только, если коэффициент трения (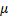) больше, чем 
, а тангенс угла наклона мотоциклиста (угла наклона линии, соединяющей точку опоры с центром масс) должен быть равен : 
.
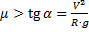Итоги
Необходимо помнить, что в неинерциальных системах отсчёта, кроме физических сил (результатов взаимодействия), появляются и не физические, равные массе на ускорение данной системы отсчёта со знаком минус