Объемы многогранников

Многогранники и объем многогранников

    Многоугольники относятся к плоским геометрическим фигурам. К объемным (трехмерным) геометрическим фигурам относятся многогранники.

    Определение. Многогранник — это геометрическое пространственное тело, ограниченное со всех сторон конечным числом плоских многоугольников (граней).

    Прямоугольный параллелепипед является многогранником. Простейший прямоугольный параллелепипед — это куб. У него все грани равны

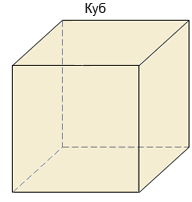
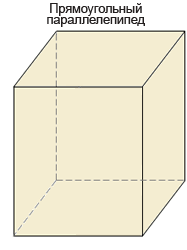
    У прямоугольного параллелепипеда каждая грань — прямоугольник, который имеет с соседней гранью общую сторону и две общие вершины.

    У параллелепипеда 8 вершин, 4 боковых прямоугольника и 2 прямоугольника в основаниях. У куба все б граней — равные квадраты. У прямоугольного параллелепипеда боковые фигуры и основания — прямоугольники. Эти прямоугольники попарно равны (равны прямоугольники оснований и две пары противолежащих прямоугольников, составляющих боковые грани). Следовательно, грани прямоугольного параллелепипеда являются прямоугольниками трех типов, различающихся размерами.

Три прямоугольника с разными размерами имеют одну общую точку — вершину параллелепипеда.

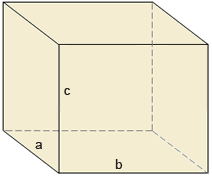
У каждой вершины параллелепипед имеет общую точку для трех отрезков, которые называются измерениями параллелепипеда (длина, ширина и высота). Три измерения на верхнем рисунке параллелепипеда выделены жирной линией.

Объем — это то количество жидкости или сыпучего материала, которое можно поместить внутрь фигуры (между граничными плоскостями).

Объем — это одна из характеристик трехмерных геометрических фигур.

Объем обозначается большой латинской буквой V («вэ»). Величины объема взаимосвязаны (одну кубическую единицу объема можно заменить ругой).

Правило. Объем прямоугольного параллелепипеда равен произведению трех его измерений.

Единицами измерения объема служат:

• а) стандартные единицы длины в кубе: 1 см³ = 1 000 мм³

1 дм³ = 1 000 см³ = 1 000 000 мм³ 1 м³ = 1 000 дм³ = 1 000 000 см³ — 1 000 000 000 мм³

1 км³ — 1 000 000 000 м³

• б) специальная единица объема (литр): 1 л = 1 дм³ = 1 000 см³.

Формула для расчета объема прямоугольного параллелепипеда: V = abc где а — длина, Ь — ширина, с — высота.

Так как у куба все измерения равны (а = Ь = с), то формула для вычисления объема куба V = а³.

Примеры

1. Вычислить объем прямоугольного параллелепипеда длиной 6 м, шириной 4 м и высотой 8 м.

Решение.

Так как длина, ширина и высота измеряются одной и той же единицей длины (м), то подставим их в формулу V=а*Ь*с и вычислим объем: V = 6 ×4 × 8 = 192 (м³)

Ответ: 192 м³.

2. Вычислите объем куба со стороной основания 10 см.

Решение.

Подставим численное значение стороны куба в формулу вычисления объема V=а³ и вычислим: V = 10 × 10×10 = 10³ = 1 000 (см³) — 1 л.

Ответ: 1 000 см³, или 1 л