Решение задач по теме "Оптика"

 Задача 1

На ри­сун­ке 1 пред­став­ле­на пло­ско­па­рал­лель­ная пла­сти­на и ука­зан ход луча через эту пла­сти­ну. Опре­де­ли­те по­ка­за­тель пре­лом­ле­ния пла­сти­ны. Ва­ри­ан­ты от­ве­та: 1. 0,67; 2. 1,33; 3. 1,5; 4. 2,0.

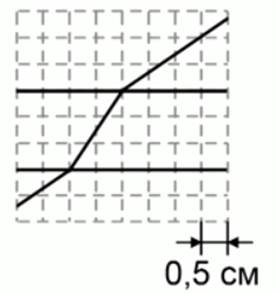
Рис. 1. Ил­лю­стра­ция к за­да­че

Ре­ше­ние

По­ка­за­тель пре­лом­ле­ния равен:

,

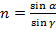где 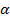 – угол па­де­ния,  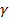– угол пре­лом­ле­ния (см. Рис. 2).

Для опре­де­ле­ния си­ну­сов дан­ных углов рас­смот­рим два пря­мо­уголь­ных тре­уголь­ни­ка (вы­де­лен­ных крас­ным цве­том на ри­сун­ке 2).

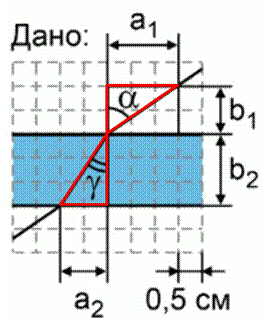
Рис. 2. Ил­лю­стра­ция к за­да­че

Из пер­во­го тре­уголь­ни­ка:

 ,

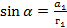где 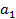 – катет, про­ти­во­ле­жа­щий углу 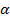;  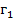– ги­по­те­ну­за.

Из вто­ро­го тре­уголь­ни­ка:

,

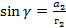где 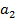 – катет, про­ти­во­ле­жа­щий углу 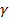;  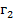– ги­по­те­ну­за.

Со­глас­но тео­ре­ме Пи­фа­го­ра:

- ги­по­те­ну­за пер­во­го тре­уголь­ни­ка:

,

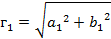где 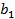 – катет, при­ле­жа­щий углу .

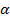- ги­по­те­ну­за вто­ро­го тре­уголь­ни­ка:

,

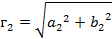где 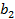 – катет, при­ле­жа­щий углу .

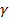На ри­сун­ке 2 видно, что:

 

 

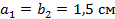
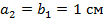
Сле­до­ва­тель­но:

 

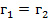
Таким об­ра­зом, по­ка­за­тель пре­лом­ле­ния равен:

 

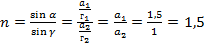
Ответ: 3. .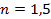

 Задача 2

На экране с по­мо­щью тон­кой линзы, фо­кус­ное рас­сто­я­ние ко­то­рой равно 36,5 см, по­лу­че­но изоб­ра­же­ние пред­ме­та с де­ся­ти­крат­ным уве­ли­че­ни­ем. Необ­хо­ди­мо найти рас­сто­я­ние от линзы до изоб­ра­же­ния.

Дано: 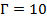 – уве­ли­че­ние;  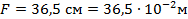– фо­кус­ное рас­сто­я­ние линзы

Найти: 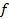 – рас­сто­я­ние от линзы до изоб­ра­же­ния

Ре­ше­ние

Фор­му­ла тон­кой линзы:

,

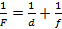где d – рас­сто­я­ние от линзы до пред­ме­та.

Уве­ли­че­ние линзы опре­де­ля­ет­ся по фор­му­ле:

 

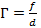
Вы­ра­зим из этой фор­му­лы рас­сто­я­ние от линзы до пред­ме­та и под­ста­вим по­лу­чен­ное зна­че­ние в фор­му­лу тон­кой линзы:

 

 

 

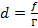
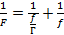
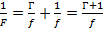
От­сю­да рас­сто­я­ние от линзы до изоб­ра­же­ния равно:

 

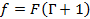
Под­ста­вим в дан­ное вы­ра­же­ние из­вест­ные зна­че­ния:

 

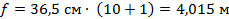
Ответ: .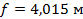

 Задача 3

Сколь­ко раз длина волны света укла­ды­ва­ет­ся в плен­ке, тол­щи­на ко­то­рой со­став­ля­ет 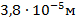? По­ка­за­тель пре­лом­ле­ния плен­ки – 1,8; длина волны в ва­ку­у­ме – 720 нм. Волна па­да­ет на плен­ку пер­пен­ди­ку­ляр­но ее плос­ко­сти.

Дано: 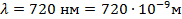 – длина волны в ва­ку­у­ме;  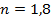– по­ка­за­тель пре­лом­ле­ния плен­ки;  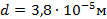– тол­щи­на плен­ки

Найти: 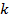 – число длин волн

Ре­ше­ние

На тол­щине плен­ки d укла­ды­ва­ет­ся число длин волн:

,

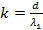где 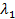 – длина волны в плен­ке.

Как из­вест­но, длина волны в ве­ще­стве (плен­ке) равна:

,

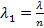где n – по­ка­за­тель пре­лом­ле­ния ве­ще­ства, 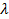 – длина волны в ва­ку­у­ме.

Сле­до­ва­тель­но:

 

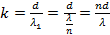
Под­ста­вим в дан­ное вы­ра­же­ние из­вест­ные зна­че­ния:

 

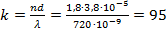
Ответ: