Построение изображений, даваемых линзами

Вы уже зна­ко­мы с ос­нов­ны­ми ме­то­ди­ка­ми, ко­то­рые поз­во­ля­ют стро­ить изоб­ра­же­ние, да­ва­е­мое лин­зой. Воз­мож­но, у вас воз­ник во­прос: по­че­му, решая за­да­чи про линзы, мы изоб­ра­жа­ем их на плос­ко­сти, ведь линза – это трех­мер­ный объ­ект? Ответ очень про­стой: как и в дру­гих раз­де­лах фи­зи­ки, в дан­ном мы при­бе­га­ем к упро­ще­ни­ям и рас­смат­ри­ва­ем толь­ко те слу­чаи, в ко­то­рых пред­мет, изоб­ра­же­ние ко­то­ро­го стро­ит­ся, можно изоб­ра­зить в виде от­рез­ка.

Любой трех­мер­ный объ­ект, в ко­неч­ном итоге, пред­став­ля­ет­ся как об­ласть про­стран­ства, огра­ни­чен­ная ко­неч­ным чис­лом от­рез­ков, и наш слу­чай легко рас­про­стра­ня­ет­ся на трех­мер­ную за­да­чу.

В силу сим­мет­рии линзы от­но­си­тель­но плос­ко­сти, про­хо­дя­щей через пред­мет и оп­ти­че­ский центр линзы, а имен­но плос­ко­сти ри­сун­ка, нам до­ста­точ­но рас­смат­ри­вать лучи, при­над­ле­жа­щие этой плос­ко­сти. Любые лучи, ко­то­рые не лежат в этой плос­ко­сти, не дадут нам ни­ка­кой ин­фор­ма­ции об изоб­ра­же­нии.

Таким об­ра­зом, ис­ход­ную по­ста­нов­ку за­да­чи можно сфор­му­ли­ро­вать так: необ­хо­ди­мо на­учить­ся стро­ить изоб­ра­же­ния пред­ме­тов, ва­рьи­руя рас­по­ло­же­ние по­след­них от­но­си­тель­но линзы.

Какие дан­ные мы хотим по­лу­чить на вы­хо­де?

1. Рас­по­ло­же­ние изоб­ра­же­ния от­но­си­тель­но линзы.

2. Яв­ля­ет­ся ли это изоб­ра­же­ние пря­мым или пе­ре­вер­ну­тым.

3. Со­от­но­ше­ние между раз­ме­ра­ми изоб­ра­же­ния и пред­ме­та (уве­ли­че­ние линзы).

4.Тип изоб­ра­же­ния (мни­мое или дей­стви­тель­ное).

 

Для на­ча­ла вспом­ним ос­нов­ные обо­зна­че­ния: 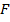 – фо­кус­ное рас­сто­я­ние линзы; d -рас­сто­я­ние от линзы до пред­ме­та; 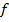– рас­сто­я­ние от линзы до изоб­ра­же­ния.

Обо­зна­чим на глав­ной оп­ти­че­ской оси ос­нов­ные точки (глав­ный фокус и точку, рас­по­ло­жен­ную на удво­ен­ном фо­кус­ном рас­сто­я­нии от линзы – 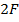). Пред­мет будем изоб­ра­жать сплош­ной стрел­кой, а изоб­ра­же­ние – пунк­тир­ной.

 

 Случай № 1

 

Пусть пред­мет на­хо­дит­ся на рас­сто­я­нии, пре­вы­ша­ю­щем двой­ной фокус (Рис. 1).

 

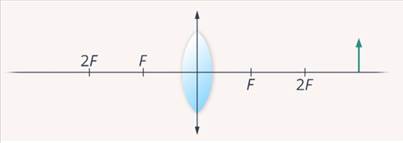
Рис. 1. Слу­чай№ 1

 

Для по­стро­е­ния изоб­ра­же­ния нам до­ста­точ­но вы­брать два луча, ис­хо­дя­щих из верх­не­го конца от­рез­ка пред­ме­та. Один из этих лучей вы­бе­рем так, чтобы он шел па­рал­лель­но глав­ной оп­ти­че­ской оси, вто­рой луч пусть идет через оп­ти­че­ский центр линзы. После пре­лом­ле­ния пер­вый луч про­хо­дит через фокус, вто­рой же не ме­ня­ет сво­е­го на­прав­ле­ния. На­хо­дим точку пе­ре­се­че­ния лучей, из нее опус­ка­ем пер­пен­ди­ку­ляр на глав­ную оп­ти­че­скую ось и по­лу­ча­ем изоб­ра­же­ние (Рис. 2).

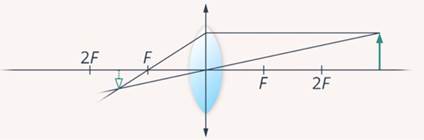
Рис. 2. Слу­чай № 1

 

В ре­зуль­та­те мы видим, что наше изоб­ра­же­ние на­хо­дит­ся между фо­ку­сом и двой­ным фо­ку­сом, яв­ля­ет­ся пе­ре­вер­ну­тым, умень­шен­ным и дей­стви­тель­ным. Тот же вывод, за ис­клю­че­ни­ем пе­ре­вер­ну­то­сти, можно по­лу­чить с по­мо­щью фор­му­лы тон­кой линзы. Вспом­ним ее:

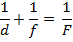
Возь­мем, что рас­сто­я­ние от пред­ме­та до линзы равно 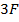.Вы­пол­нив про­стые ал­геб­ра­и­че­ские пре­об­ра­зо­ва­ния, по­лу­чим, что:

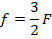
Дан­ная ве­ли­чи­на мень­ше удво­ен­но­го фо­кус­но­го рас­сто­я­ния и боль­ше фо­кус­но­го, как и было по­ка­за­но на ри­сун­ке, изоб­ра­же­ние на­хо­дит­ся между фо­ку­сом и двой­ным фо­ку­сом. Уве­ли­че­ние, как из­вест­но, можно вы­чис­лить по фор­му­ле:

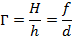
В дан­ном слу­чае мы по­лу­ча­ем, что 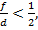 и изоб­ра­же­ние по­лу­ча­ет­ся мень­ше, чем пред­мет по раз­ме­ру.

 Случай № 2

 

Пред­мет на­хо­дит­ся точно в двой­ном фо­ку­се, вы­пол­ня­ем по­стро­е­ние с теми же лу­ча­ми, опус­ка­ем пер­пен­ди­ку­ляр – по­лу­ча­ем изоб­ра­же­ние (Рис. 2).

 

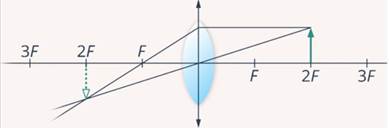
Рис. 3. Слу­чай № 2

Видим, что изоб­ра­же­ние тоже по­па­да­ет в двой­ной фокус, яв­ля­ет­ся пе­ре­вер­ну­тым и по раз­ме­ру сов­па­да­ет с пред­ме­том. Про­ве­рим ре­зуль­тат: при­ме­нив фор­му­лу тон­кой линзы, по­лу­ча­ем:

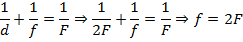
Уве­ли­че­ние же равно еди­ни­це. То есть изоб­ра­же­ние и пред­мет имеют оди­на­ко­вые раз­ме­ры.

 Случай № 3

 

Пред­мет на­хо­дит­ся между двой­ным фо­ку­сом и глав­ным. Вы­пол­нив по­стро­е­ние, можно уви­деть, что в этом слу­чае изоб­ра­же­ние по­лу­ча­ет­ся уве­ли­чен­ным, пе­ре­вер­ну­тым и на­хо­дит­ся за двой­ным фо­ку­сом линзы (Рис. 4).

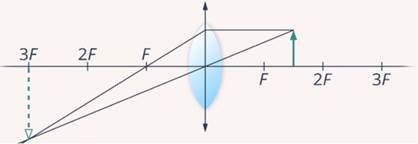
Рис. 4. Слу­чай № 3

До­ка­жем ал­геб­ра­и­че­ски. Пред­по­ло­жим, что 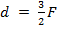, под­став­ля­ем зна­че­ние и по­лу­ча­ем, что 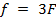, а .

 

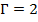Все по­лу­чен­ные выше ре­зуль­та­ты на­хо­дят при­ме­не­ние в оп­ти­че­ских при­бо­рах. Один из таких при­бо­ров – фо­то­ап­па­рат.

 

Схема устрой­ства фо­то­ап­па­ра­та

 

Фо­то­ап­па­рат со­сто­ит из объ­ек­ти­ва и кор­пу­са со све­то­не­про­ни­ца­е­мы­ми стен­ка­ми. Объ­ек­тив по­ме­ща­ет­ся у пе­ред­ней стен­ки, а у зад­ней по­ме­ща­ет­ся све­то­чув­стви­тель­ный эле­мент, это может быть плен­ка, как в ста­рых фо­то­ап­па­ра­тах, или фо­то­ди­од­ная мат­ри­ца (Рис. 5).

Рис. 5. Схема устрой­ства фо­то­ап­па­ра­та

Как пра­ви­ло, при съем­ке фо­то­гра­фи­ру­е­мый объ­ект на­хо­дит­ся на рас­сто­я­нии, го­раз­до боль­шем фо­кус­но­го рас­сто­я­ния объ­ек­ти­ва. Вслед­ствие этого изоб­ра­же­ние на фо­то­эле­мен­те по­лу­ча­ет­ся пе­ре­вер­ну­тым и умень­шен­ным. Для того чтобы по­лу­чить от­чет­ли­вое изоб­ра­же­ние объ­ек­та, есть воз­мож­ность пе­ре­дви­гать объ­ек­тив от­но­си­тель­но зад­ней стен­ки кор­пу­са.

В за­ви­си­мо­сти от пред­на­зна­че­ния при­ме­ня­ют раз­лич­ные кон­струк­ции фо­то­ап­па­ра­тов, но наи­бо­лее важ­ной ча­стью яв­ля­ет­ся объ­ек­тив. Имен­но им в ос­нов­ном опре­де­ля­ет­ся ка­че­ство сним­ка. В про­стей­шем слу­чае фо­то­объ­ек­тив может яв­лять­ся со­би­ра­ю­щей лин­зой, од­на­ко такая линза дает от­чет­ли­вое изоб­ра­же­ние лишь в очень огра­ни­чен­ном ко­ли­че­стве слу­ча­ев. Фо­то­объ­ек­ти­вы, ко­то­рые дают ка­че­ствен­ное изоб­ра­же­ние, обыч­но со­сто­ят из несколь­ких линз и пред­став­ля­ют собой до­воль­но слож­ную кон­струк­цию (Рис. 6).

Рис. 6. Фо­то­объ­ек­тив в раз­ре­зе

Для того чтобы ре­гу­ли­ро­вать све­то­вой поток, по­сту­па­ю­щий в фо­то­ап­па­рат, объ­ек­тив снаб­жа­ет­ся диа­фраг­мой, диа­метр ко­то­рой можно из­ме­нять, таким об­ра­зом меняя раз­ме­ры от­вер­стия.

 Случай № 4

Пред­мет на­хо­дит­ся четко в фо­ку­се линзы. Вы­пол­ня­ем по­стро­е­ние и видим, что лучи после пре­лом­ле­ния идут па­рал­лель­но, то есть не пе­ре­се­ка­ют­ся. Изоб­ра­же­ния в этом слу­чае нет (Рис. 7).

 

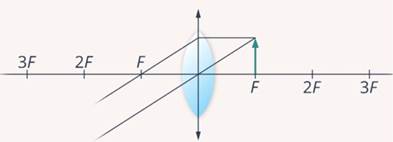
Рис. 7. Слу­чай № 4

Как до­ка­зать этот же факт ал­геб­ра­и­че­ски? Мы видим, что 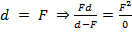, а такая дробь не су­ще­ству­ет. Таким об­ра­зом, в дан­ном слу­чае изоб­ра­же­ния не будет.

 Случай № 5

Пред­мет на­хо­дит­ся между лин­зой и фо­ку­сом. Про­стые по­стро­е­ния по­ка­зы­ва­ют, что после по­стро­е­ния лучи рас­хо­дят­ся. Дей­стви­тель­но­го изоб­ра­же­ния в этом слу­чае на­блю­дать­ся не будет, од­на­ко пе­ре­се­ка­ют­ся про­дол­же­ния лучей. А мы уже знаем, что в таких слу­ча­ях глаз пре­об­ра­зу­ет изоб­ра­же­ние так, что мы видим мни­мое изоб­ра­же­ние пред­ме­та. На­хо­дим точку пе­ре­се­че­ния про­дол­же­ний лучей и по­лу­ча­ем мни­мое изоб­ра­же­ние. Оно по­лу­ча­ет­ся уве­ли­чен­ным и пря­мым. Имен­но этот слу­чай имеет место, когда мы поль­зу­ем­ся оч­ка­ми или лупой. Итак, ал­геб­ра­и­че­ское до­ка­за­тель­ство того же факта: под­ста­вив зна­че­ние (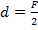) по­лу­ча­ем: 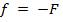и .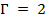

 

Лупа

 

Для на­ча­ла вспом­ним, как устро­ен че­ло­ве­че­ский глаз (Рис. 8).

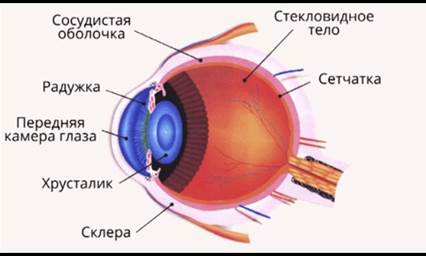
Рис. 8. Стро­е­ние че­ло­ве­че­ско­го глаза

Про­стей­шим при­бо­ром для во­ору­же­ния глаза яв­ля­ет­ся лупа. В ка­че­стве лупы при­ме­ня­ют­ся со­би­ра­ю­щие линзы с фо­кус­ным рас­сто­я­ни­ем 10–100 мм.

Лупа по­ме­ща­ет­ся перед гла­зом, по воз­мож­но­сти близ­ко к нему, а рас­смат­ри­ва­е­мый пред­мет – на рас­сто­я­нии немно­го боль­шем, чем фо­кус­ное рас­сто­я­ние лупы. По­стро­е­ние изоб­ра­же­ния, да­ва­е­мо­го лупой, уже было рас­смот­ре­но на уроке, оно по­лу­ча­ет­ся мни­мым, пря­мым и уве­ли­чен­ным.

Рас­смот­рим ход лучей к пред­ме­ту, рас­смат­ри­ва­е­мо­му через лупу (Рис. 9).

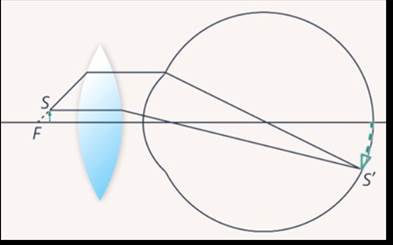
Рис. 9. По­стро­е­ние изоб­ра­же­ния, да­ва­е­мо­го лупой

Лучи, ис­хо­дя­щие из точки S, сна­ча­ла пре­лом­ля­ют­ся в лупе, затем в пре­лом­ля­ю­щих сре­дах глаза и со­би­ра­ют­ся в неко­то­рой точке на сет­чат­ке.

В той же самой точке со­бра­лись бы лучи, если бы лупы не было, а ис­точ­ник на­хо­дил­ся бы в дру­гой точке, такой, как будто бы глаз непо­сред­ствен­но рас­смат­ри­вал пред­мет уве­ли­чен­ных раз­ме­ров, на­хо­дя­щий­ся на со­от­вет­ству­ю­щем рас­сто­я­нии от него.

 

По­стро­е­ние изоб­ра­же­ний да­ва­е­мых рас­се­и­ва­ю­щей лин­зой

Рас­смот­рим те же слу­чаи, что и с со­би­ра­ю­щей лин­зой (Рис. 10).

Слу­чай № 1 – за двой­ным фо­ку­сом

Слу­чай № 2 – в двой­ном фо­ку­се

Слу­чай № 3 – пред­мет между фо­ку­сом и двой­ным фо­ку­сом

Слу­чай № 4 – пред­мет в фо­ку­се

Слу­чай № 5 – пред­мет между фо­ку­сом и лин­зой

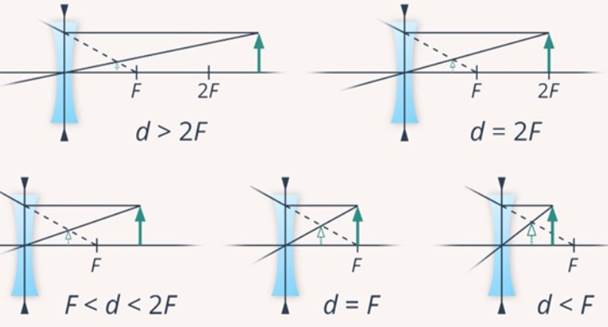
Рис. 10. По­стро­е­ние изоб­ра­же­ний рас­се­и­ва­ю­щей линзы

Как мы видим, во всех си­ту­а­ци­ях изоб­ра­же­ние по­лу­ча­ет­ся мни­мым, умень­шен­ным и пря­мым. По­про­буй­те сами до­ка­зать эти утвер­жде­ния ал­геб­ра­и­че­ски, ис­поль­зуя фор­му­лы тон­кой линзы.

 Задача № 1

Со­би­ра­ю­щая линза дает на экране изоб­ра­же­ние лам­поч­ки, уве­ли­чен­ное в два раза (Рис. 11.1). Когда линзу по­дви­ну­ли на рас­сто­я­ние 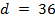 см ближе к экра­ну, то она дала изоб­ра­же­ние, вдвое умень­шен­ное (Рис. 11.2). Най­ди­те фо­кус­ное рас­сто­я­ние линзы.

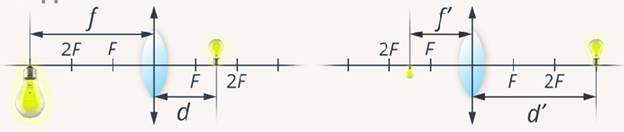
Рис. 11.1, 11.2. За­да­ча № 1

Ре­ше­ние: из­на­чаль­но линза да­ва­ла уве­ли­чен­ное в два раза изоб­ра­же­ние лам­поч­ки; вспом­нив по­лу­чен­ные нами ранее ре­зуль­та­ты, мы можем утвер­ждать, что пред­мет на­хо­дит­ся между 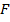 и 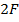, а изоб­ра­же­ние – за двой­ным фо­ку­сом линзы. Зна­ние уве­ли­че­ния дает нам, что 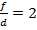. После сме­ще­ния линзы изоб­ра­же­ние стало вдвое мень­ше по раз­ме­рам. Обо­зна­чив через  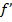и 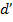 рас­сто­я­ние до изоб­ра­же­ния и пред­ме­та после сме­ще­ния линзы, можем утвер­ждать, что пред­мет на­хо­дит­ся за двой­ным фо­ку­сом, а изоб­ра­же­ние – между фо­ку­сом и двой­ным фо­ку­сом, кроме того: .

 

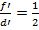Рас­сто­я­ние от пред­ме­та до изоб­ра­же­ния не из­ме­ни­лось, из­ме­ни­лись толь­ко рас­сто­я­ния от линзы до пред­ме­та и экра­на. При­чем из усло­вия нам из­вест­но, как имен­но они из­ме­ни­лись, так как нам дано, что линзу по­дви­ну­ли на 36 см. Таким об­ра­зом, по­лу­ча­ем сле­ду­ю­щее со­от­но­ше­ние:

 

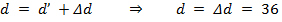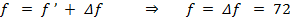cм
cм

Ис­поль­зо­вав фор­му­лу тон­кой линзы, при­хо­дим к сле­ду­ю­щей си­сте­ме урав­не­ний, из ко­то­рой вы­ра­жа­ем фо­кус­ное рас­сто­я­ние:

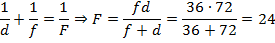
Ответ: 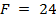 см.

 Итоги урока

Мы на­учи­лись де­лать вы­во­ды об изоб­ра­же­нии, не вы­пол­няя по­стро­е­ний или вы­чис­ле­ний; нам до­ста­точ­но знать, на каком рас­сто­я­нии от линзы на­хо­дит­ся пред­мет.