Сообщение от Kris Kim
Параллелограмм, все стороны которого равны называется ромбом.
- Диагональ ромба является его осью симметрии. Диагонали взаимно перпендикулярны. Диагонали являются биссектрисами углов.
- Площадь:
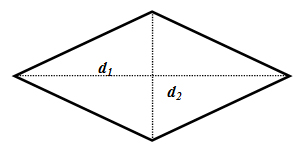
Параллелограмм, все стороны которого равны называется ромбом.

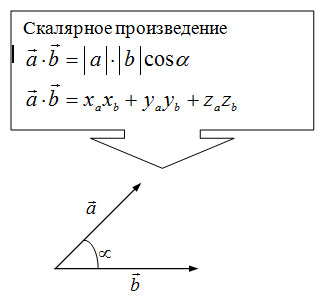
Скалярным произведением двух векторов и
называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними.
Среднее арифметическое:
Среднее геометрическое:
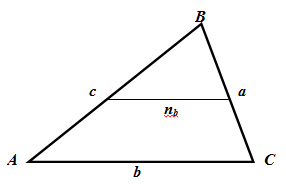
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
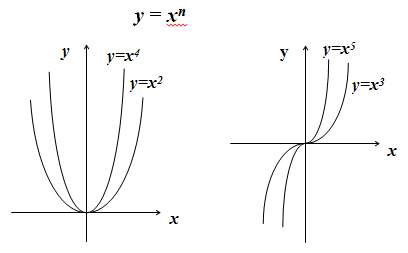
Степенной функцией с вещественным показателем a называется функция y = x n , x > 0.
Заметим, что для натуральных n степенная функция определена на всей числовой оси.
Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x.
Основные значения тригонометрических функций углов I четверти приведены в таблице.
Приведенное квадратное уравнение: x2 + px + q = 0
x1 + x2 = - p
x1× x2 = q
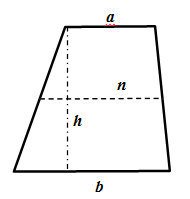
Четырёхугольник, у которого две стороны параллельны, а другие не параллельны, называется трапецией.
Углом называется фигура, состоящая из двух лучей с общим началом и ограниченной ими части плоскости. Точка, из которой выходят ограничивающие угол лучи, называется вершиной угла, а сами лучи - сторонами угла.
Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
При пересечении двух параллельных прямых третьей, называемой секущей:
Пусть S(t) - уравнение движения материальной точки,
где S – путь, t – время движения.
Тогда: ,
где v – скорость, a - ускорение.
Уравнение касательной к графику функции
в точке x0 имеет вид: ,
где - угловой коэффициент касательной.

Замечание:
В уравнении прямой линии: , параметр - называется угловым коэффициентом, и две прямые параллельны, если их угловые коэффициенты равны.
Квадрат суммы (a + b)2 = a2 + 2ab + b2
Квадрат разности (a - b)2 = a2 - 2ab + b2
Разность квадратов a2 – b2 = (a + b)(a – b)
Куб суммы (a + b)3 = a3 + 3a2b + 3ab2 + b3
Куб разности (a - b)3 = a3 - 3a2b + 3ab2 - b3
Сумма кубов a3 + b3 = (a + b)( a2 - ab + b2)
Разность кубов a3 – b3 = (a – b)( a2 + ab + b2)
Функция модуль задается уравнением y = | x |.
График функция модуль состоит из биссектрис первого и второго координатных углов
Свойства:
Функция модуль является четной функцией.
Производная функции модуль в точке x=0 не существует.
График функции модуль симметричен относительно оси ординат.
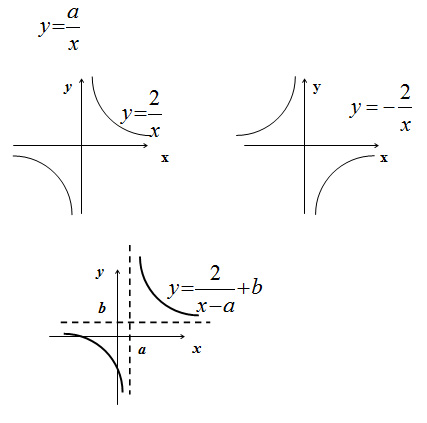
Переменные x и y связаны обратно пропорциональной зависимостью , где
, k - коэффициент обратной пропорциональности.
Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны. В окружности равные хорды равноудалены от центра окружности.

Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды:

Центральный угол — это угол, вершина которого находится в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.
Определение:
Примеры:
Свойства:
График четной функции симметричен относительно оси Oy.
График нечетной функции симметричен относительно начала системы координат О.