Неравенства с параметрами

Решение неравенств с параметром.

Неравенства, которые имеют вид ax > b, ax < b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются линейными неравенствами.

Принципы решения линейных неравенств с параметром очень схожи с принципами решения линейных уравнений с параметром.

Пример 1.

Решить неравенство 5х – а > ax + 3.

Решение.

Для начала преобразуем исходное неравенство:

5х – ах > a + 3, вынесем за скобки х в левой части неравенства:

(5 – а)х > a + 3. Теперь рассмотрим возможные случаи для параметра а:

Если a > 5, то x < (а + 3) / (5 – а).

Если а = 5, то решений нет.

Если а < 5, то x > (а + 3) / (5 – а).

Данное решение и будет являться ответом неравенства.

Пример 2.

Решить неравенство х(а – 2) / (а – 1) – 2а/3 ≤ 2х – а при а ≠ 1.

Решение.

Преобразуем исходное неравенство:

х(а – 2) / (а – 1) – 2х ≤ 2а/3 – а;

-ах/(а – 1) ≤ -а/3. Домножим на (-1) обе части неравенства, получим:

ах/(а – 1) ≥ а/3. Исследуем возможные случаи для параметра а:

1 случай. Пусть a/(а – 1) > 0 или а € (-∞; 0)ᴗ(1; +∞). Тогда x ≥ (а – 1)/3.

2 случай. Пусть a/(а – 1) = 0, т.е. а = 0. Тогда x – любое действительное число.

3 случай. Пусть a/(а – 1) < 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

Ответ: х € [(а – 1)/3; +∞) при а € (-∞; 0)ᴗ(1; +∞);  х € [-∞; (а – 1)/3] при а € (0; 1);  х € R при а = 0.

Пример 3.

Решить неравенство |1 + x| ≤ аx относительно х.

Решение.

Из условия следует, что правая часть неравенства ах должна быть не отрицательна, т.е. ах ≥ 0. По правилу раскрытия модуля из неравенства |1 + x| ≤ аx имеем двойное неравенство

-ах ≤ 1 + x ≤ аx. Перепишем результат в виде системы:

{аx ≥ 1 + x;  {-ах ≤ 1 + x.

Преобразуем к виду:

{(а – 1)x ≥ 1;  {(а + 1)х ≥ -1.

Исследуем полученную систему на интервалах и в точках (рис. 1):

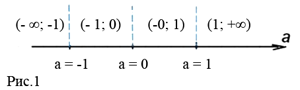
При а ≤ -1 х € (-∞; 1/(а – 1)].

При -1 < а < 0 x € [-1/(а – 1); 1/(а – 1)].

При а = 0 x = -1.

При 0 < а ≤ 1 решений нет.

Графический метод решения неравенств

Построение графиков значительно упрощает решение уравнений, содержащих параметр. Использование графического метода при решении неравенств с параметром еще нагляднее и целесообразнее.

Графическое решение неравенств вида f(x) ≥ g(x) означает нахождение значений переменной х, при которых график функции f(x) лежит выше графика функции g(x). Для этого всегда необходимо найти точки пересечения графиков (если они существуют).

Пример 1.

Решить неравенство |x + 5| < bx.

Решение.

Строим графики функций у = |x + 5| и у = bx (рис. 2). Решением неравенства будут те значения переменной х, при которых график функции у = |x + 5| будет находиться ниже  графика функции у = bx.

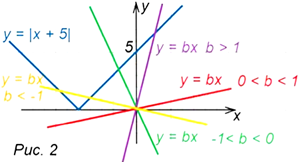
На рисунке видно:

1. При b > 1 прямые пересекаются. Абсцисса точки пересечения графиков этих функций есть решение уравнения х + 5 = bx, откуда х = 5/(b – 1). График у = bx находится выше при х из интервала (5/(b – 1); +∞), значит это множество и есть решение неравенства.
2. Аналогично находим, что при -1 < b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).
3. При b ≤ -1 x € (-∞; 5/(b – 1)).
4. При 0 ≤ b ≤ 1 графики не пересекаются, а значит, и решений у неравенства нет.

Ответ: x € (-∞; 5/(b – 1)) при b ≤ -1;  x € (-5/(b + 1); 5/(b – 1)) при -1 < b < 0;  решений нет при 0 ≤ b ≤ 1; x € (5/(b – 1); +∞) при b > 1.

Пример 2.

Решить неравенство а(а + 1)х > (a + 1)(a + 4).

Решение.

1. Найдем «контрольные » значения для параметра а: а₁ = 0, а₂ = -1.
2. Решим данное неравенство на каждом подмножестве действительных чисел: (-∞; -1); {-1}; (-1; 0); {0}; (0; +∞).

a) a < -1, из данного неравенства следует, что х > (a + 4)/a;

b) a = -1, тогда данное неравенство примет вид 0·х > 0 – решений нет;

c) -1 < a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, тогда данное неравенство имеет вид 0 · х > 4 – решений нет;

e) a > 0, из данного неравенства следует, что х > (a + 4)/a.

Пример 3.

Решить неравенство |2 – |x|| < a – x.

Решение.

Строим график функции у = |2 – |x|| (рис. 3) и рассматриваем все возможные случаи расположения прямой у = -x + а.

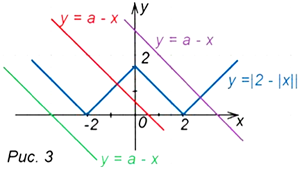
Ответ: решений у неравенства нет при а ≤ -2;  x € (-∞; (а – 2)/2) при а € (-2; 2]; x € (-∞; (a + 2)/2) при a > 2.

При решении различных задач, уравнений и неравенств с параметрами открывается значительное число эвристических приемов, которые потом с успехом могут быть применены в любых других разделах математики.

Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры. Именно поэтому, овладев методами решения задач с параметрами, вы успешно справитесь и с другими задачами.