Числовые промежутки. Пересечение и объединение числовых промежутков

Отметим на координатной прямой точки с координатами -3 и 2. Если точка расположена между ними, то ей соответствует число, которое больше -3 и меньше 2. Верно и обратное: если число х удовлетворяет условию -3<x<2 , то оно изображается точкой, лежащей между точками с координатами -3 и 2.

Множество всех чисел, удовлетворяющих условию -3<x<2, называется числовым промежутком или просто промежутком от -3 до 2 и обозначается так: (-3;2).

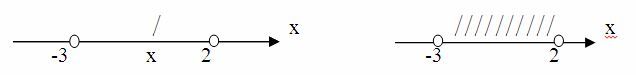
На рисунках изображены множество чисел х, для которых выполняется неравенство х<10 и х≤10. Эти множества представляют собой промежутки, обозначаемые соответственно (-∞; 10) и (-∞; 10]. Читается так: число х принадлежит промежутку от минус бесконечности (-∞) до 10 (х<10) и число х принадлежит промежутку от минус бесконечности (-∞) до 10, включая число 10 (х≤10). Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В. Промежуток [3;5] является пересечением промежутков [-1;5] и [3;7]. Это можно записать так: [-1;5]∩[3;7]=[3;5].

Промежутки [0;4] и [6;10] не имеют общих элементов. Если множество не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0;4]∩[6;10]=0.

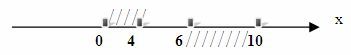
Объединение числовых промежутков

Каждое число из промежутка [1;7] принадлежит хотя бы одному из промежутков [1;5] и [3;7], то есть, либо промежутку [1;5], либо промежутку [3;7], либо им обоим. 

Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают AB.

Промежуток [1;7] является объединением промежутков [1;5] и [3;7]. Это можно записать так: 

Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество не является  промежутком.

1. Числовым промежутком называется множество всех чисел, удовлетворяющих неравенству.
2. Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.
3. Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В.
4. Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают .

Вопросы к конспектам