Соотношение неопределенностей Гейзенберга. Два пути развития квантовой механики
В 1925 году де Бройль выдвинул теорию о том, что все микроэлементы обладают корпускулярно-волновым дуализмом. Уравнение де Бройля связывает длину волны и импульс объекта микромира.
Гейзенберг задумался, что если рассмотреть классический случай, то любая частица имеет определенную массу, координату, импульс. Но если частица имеет определенный импульс, то она описывается я в виде волны, а волна не имеет локализации. И возникает вопрос: какие законы применять в данном случае? Это был первый путь развития квантовой механики. См. Рис. 1.

Рис. 1
С точки зрения квантовой механики не понятно, что такое траектория движения. В механике: траектория – множество точек, в которых оказалось тело в тот или иной момент времени.
Пусть имеется фотон, который падает на поверхность, частично отражается и частично проходит через поверхность. Но фотон не может разделиться, тогда он либо отражается, либо проходит через поверхность. А сказать точно, что случится с фотоном, когда он достигнет этой отражающей поверхности, нельзя. См. Рис. 2.
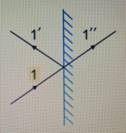
Рис. 2
Пусть имеется электрон, который двигается с каким-то импульсом. Для того чтобы найти положение электрона в пространстве и измерить его импульс, необходимо послать один фотон, чтобы он провзаимодействовал с электроном и, отраженный от него, нес с собой информацию об электроне. Вследствие дифракции света невозможно применять законы прямолинейного распространения в случае, если предметы имеют размеры порядка длины волны света. Поэтому неопределенность определения координаты заведомо примерно равна длине волны фотона. После взаимодействия с фотоном импульс электрона меняется.
В 1925 году Гейзенберг сформулировал принцип неопределенности Гейзенберга: см. Рис. 3
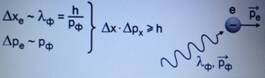
Рис. 3
Это соотношение относится ко всем канонически сопряженным величинам.
К каноническим величинам относятся: см. Рис. 4
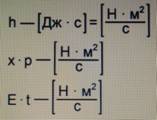
Рис. 4
Гейзенберг доказал, что неопределенность координаты, умноженная на неопределенность проекции импульса по соответствующей координате, не может быть меньше квантовой постоянной Планка. Такое же соотношение неопределенности справедливо и для неопределенности энергии и неопределенности времени.
Принцип неопределенности Гейзенберга – это основное уравнение квантовой механики.
Ответвление механики, которое организовал Гейзенберг, – матричная механика.
Применим соотношение Гейзенберга к атому водорода (Рис. 5).

Рис. 5
r – радиус атома
p – импульс электрона
ро – импульс, при котором энергия будет иметь минимальное значение
Е – энергия электрона в атоме
Этим было доказано, что электрон никогда не может упасть на ядро.
Из соотношения неопределенности Гейзенберга для атома водорода, что: см. Рис. 6

Рис. 6
Е1 – энергия электрона на первом уровне в атоме водорода
Гейзенберг составил весь спектр атома водорода и не только. Матричная механика Гейзенберга в сочетании с принципом Паули объяснила все трудности, с которыми столкнулась теория Бора. Было объяснено строение всех атомов, была развита квантовая теория твердых тел и т. д.
В 1926 году начался второй путь квантовой механики с волновой механики, которую начал развивать Шредингер.
Каждому объекту микромира сопоставляется определенная длина волны. Шредингер сказал, что если объект имеет длину волны, то он должен описываться волновой функцией. См. Рис. 7.
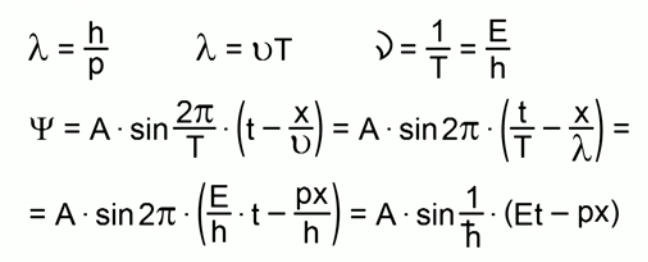
Рис. 7
А – амплитуда
V – скорость колебания
Е – энергия
Данное уравнение справедливо только для незаряженной частицы.
Шредингер доказал, что для любой заряженной частицы волновая функция должна иметь комплексный вид.
Данная функция позволяет определить вероятность нахождения частицы в той или иной области пространства.
Основное уравнение волновой механики (при фиксированном t): см. Рис. 8
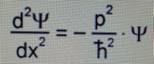
Рис. 8
В волновой механике вводятся операторы физических величин, которые, будучи примененными к пси–функции, позволяют вычислить все собственные значения, интересующие нас о частицах микромира (координату, импульс, энергию и т. д.).
Таким образом квантовая механика развивалась двумя путями, а потом Гейзенберг доказал, что и матричная квантовая механика, и волновая квантовая механика приходят к совершенно одинаковым результатам по всем вопросам и отличаются только математическим аппаратом.
