Решение задач по теме «Модель атома Н. Бора»
Задача 1
Определите скорость v и ускорение a электрона на первой боровской орбите, радиус которой определяется формулой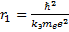 
, где 
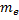и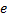 
– масса и заряд электрона; 
.
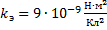Дано: 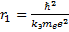– формула радиуса первой боровской орбиты; 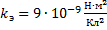– коэффициент пропорциональности закона Кулона; 
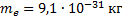– масса электрона; 
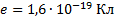– заряд электрона (
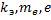– постоянные величины)
Найти: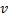 
– скорость электрона, 
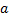– ускорение электрона
Решение
В формуле радиуса первой боровской орбиты:
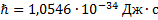– квантовая постоянная Планка
Радиус окружности, по которому происходит движение, равен:
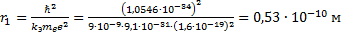
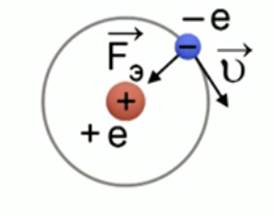
Рис. 1. Иллюстрация к задаче №1
Согласно модели Бора, вокруг ядра атома водорода, заряд которого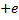 
, вращается электрон, заряд которого 
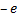(см. Рис. 1). Вращение происходит за счёт силы электрического притяжения электрона к ядру. Эта сила, по закону Кулона, равна:
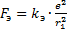
Также эта сила является центростремительной, то есть:
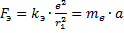
Следовательно, ускорение равно:
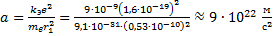
Центростремительное ускорение равно:
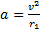
Отсюда скорость равна:
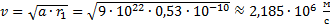
Ответ: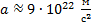 
; 
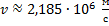
Задача 2
Найти силу электрического тока, который вызывает электрон, двигаясь по первой боровской орбите.
Дано: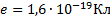 
– заряд электрона; 
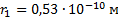– радиус орбиты; 
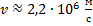– скорость электрона (найдена в задаче 1)
Найти: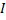 
– силу тока
Решение
Известно, что сила тока равна:
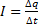
Для данной задачи:
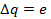
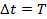– период обращения электрона
Период обращения электрона равен:
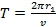
Следовательно, сила тока, возникающего при движении электрона по орбите радиусом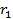 
со скоростью 
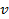, равна:
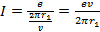
Подставим в данное выражение известные данные:
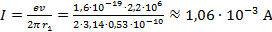
Ответ: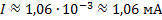 
Задача 3
Найти максимальную частоту, максимальную длину волны и максимальный импульс фотона в видимой части спектра, излучённого при переходе электрона на второй энергетический уровень в атоме водорода.
Дано: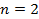 
– второй энергетический уровень; 
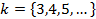– энергетические уровни, с которых может осуществляться переход электрона; 
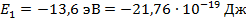– энергия на первом уровне; 
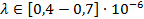м – видимая область спектра; 
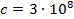– скорость света
Найти: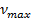 
– максимальную частоту фотона; 
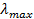– максимальную длину волны фотона; 
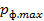– максимальный импульс фотона
Решение
Согласно второму постулату Бора:
,
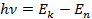где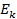 
и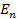 
– энергии стационарных состояний атома соответственно до и после излучения фотона; 
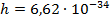– постоянная Планка; 
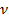– частота излучения фотона.
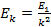
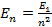
Следовательно, частота излучения фотона равна:
Частота и длина волны связаны следующим соотношением:
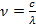
Зная световой диапазон в длинах волн (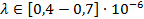), можно вычислить максимальное значение частоты кванта, который принадлежит световому диапазону:
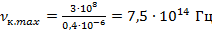
Более высокие частоты относятся к ультрафиолетовой части спектра и человеческим глазом не фиксируются.
Минимальное значение частоты при излучении будет при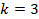 
:
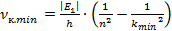
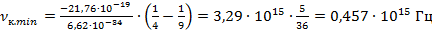
Подставим данное значение в формулу связи между длиной волны и частотой. Если частота минимальная, то значение длины волны будет максимальное:
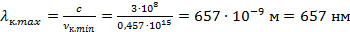
Данное значение входит в световой диапазон – это красная линия в излучении атома водорода.
Для того чтобы вычислить максимальное значение частоты фотона в видимой части спектра, необходимо подставлять значения k от 4-х и выше.
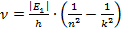
Если подставить значение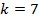 
, то мы выходим за диапазон видимой части спектра, поэтому максимальное значение 
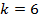. Именно для этого значения k находим максимальное значение частоты фотона:
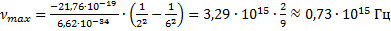
Мы попали в световой диапазон, так как он ограничивается значением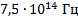 
.
Полученная максимальная частота соответствует минимальной длине волны, равной:
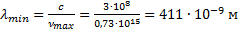
Минимальная длина волны была найдена для определения максимального импульса фотона.
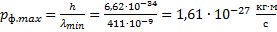
Ответ: 
; 
; 
.