Решение задач на тему "Законы постоянного тока"
1. Задача №1
Условие первой задачи звучит следующим образом. Какова длина медного цилиндрического проводника, если при его подключении в цепь с напряжением в 1 В на время 15 с его температура увеличится на 10 К?
Так как ничего не сказано о каком-либо другом действии тока, значит, считаем, что вся энергия тока идет в выделение тепла.
Пользуясь знаниями из раздела молекулярной физики, запишем, какое количество теплоты требуется для нагревания указанного количества меди на указанное количество градусов:
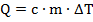
Здесь: 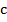 – удельная теплоемкость меди (табличная величина);
– удельная теплоемкость меди (табличная величина); 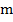 – масса провода;
– масса провода; 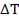 – прирост температуры.
– прирост температуры.
C дугой стороны запишем то же самое количество теплоты, но с учетом того, что именно столько выделилось в проводах в результате протекания тока. То есть воспользуемся законом Джоуля-Ленца:
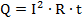
Но с учетом того, какие данные нам известны по условию, целесообразнее будет записать эту формулу в виде:
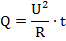
Так как эти две величины являются одним и тем же, только записанными в разном виде (сколько тепла выделилось при прохождении тока, столько и пошло на нагревание медных проводов, потерями в окружающую среду можем пренебречь), уравняем их:
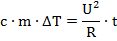
Распишем теперь все неизвестные множители на известные или табличные величины.
Распишем массу меди, как:
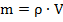
Здесь: 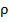 – плотность меди (табличная величина);
– плотность меди (табличная величина); 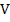 – объем проводника
– объем проводника
Так как проводник цилиндрический, можем расписать объем:
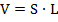
Здесь: 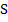 – площадь сечения проводника;
– площадь сечения проводника; 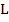 – его длина
– его длина
Также следует расписать сопротивление цилиндрического проводника по соответствующей формуле:
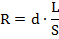
Здесь: 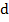 – удельное сопротивление меди (табличная величина)
– удельное сопротивление меди (табличная величина)
Подставим теперь все формулы в главное уравнение:
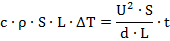
Сократив площадь сечения и выразив длину из этого выражения, мы получим формулу для финального подсчета:
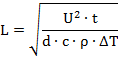
Подставив данные из условия и табличные данные, получаем:
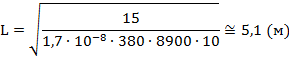
Ответ: 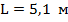
2. Задача №2
В схеме, указанной на рисунке 1:
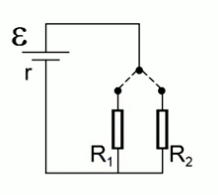
Рис. 1.
Ключ переключается между двумя резисторами, сопротивления которых равны: 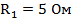 ,
, 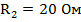 . Причем известно, что выделяемая мощность в одном и другом случае одинакова. Найти внутреннее сопротивление источника.
. Причем известно, что выделяемая мощность в одном и другом случае одинакова. Найти внутреннее сопротивление источника.
Для составления базового уравнения воспользуемся тем фактом, что мощность на каждом резисторе одна и та же:
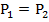
И воспользуемся формулой для мощности в удобном для нас виде:
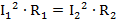
Теперь воспользуемся законом Ома для полной цепи, чтобы расписать силу тока:
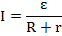
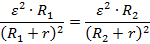
После сокращения одинаковой ЭДС получим уравнение с одним неизвестным:
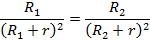
Далее решаем математическое уравнение любым удобным способом:
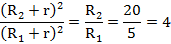
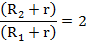
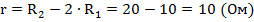
Ответ: 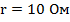
3. Вставка 1. Электрическая цепь, содержащая электроемкость
В цепи, указанной на рисунке 2, между обкладками конденсатора наблюдается электрическое поле напряженностью 4 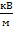 . Определить ЭДС источника, если расстояние между пластинами конденсатора – 2 мм, сопротивление резистора – 8 Ом, а внутреннее сопротивление источника – 1 Ом.
. Определить ЭДС источника, если расстояние между пластинами конденсатора – 2 мм, сопротивление резистора – 8 Ом, а внутреннее сопротивление источника – 1 Ом.
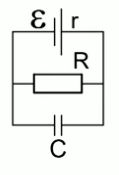
Рис. 2.
Самое главное – помнить, что так как на схеме показан источник постоянного тока, конденсатор на схеме эквивалентен обрыву, и через него ток не идет.
Для нахождения ЭДС запишем закон Ома для полной цепи:
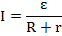
Из имеющихся данных становится понятно, что для нахождения ЭДС обязательно нужно знать значение силы тока в цепи. Для его нахождения мы теперь уже рассмотрим только внешнюю цепь и запишем закон Ома для участка цепи:
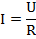
Так как конденсатор и резистор соединены параллельно, то на резисторе такое же напряжение, как и на конденсаторе. Последнее мы можем найти, воспользовавшись формулой из электростатики для однородного поля (которое и создается между обкладками конденсатора):
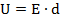
Подставим теперь все выражение в закон Ома для полной цепи:
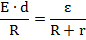
Выразим теперь ЭДС из этого уравнения:
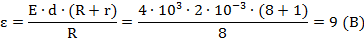
Ответ: 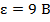
4. Вставка 2. Задачи на правила Кирхгофа
В схеме, изображенной на рисунке 3, источники обладают следующими характеристиками: 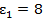 В,
В, 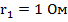 ;
; 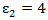 В,
В, 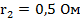 . Сопротивление резистора равно 5 Ом. Найти силу тока, протекающего через резистор.
. Сопротивление резистора равно 5 Ом. Найти силу тока, протекающего через резистор.
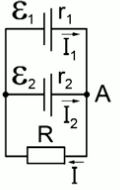
Рис. 3.
Для того чтобы решить задачу методом Кирхгофа, необходимо для удобства отметить направление течения токов.
Воспользуемся первым правилом Кирхгофа для узла А:
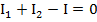
Так как токи 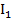 и
и 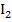 в узел входят, а ток
в узел входят, а ток 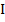 выходит из него.
выходит из него.
Для нахождения токов 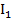 и
и 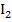 воспользуемся теперь дважды вторым правилом Кирхгофа.
воспользуемся теперь дважды вторым правилом Кирхгофа.
Рассмотрим контур, включающий в себя сопротивление R и источник 1. Согласно правилу, сумма падений напряжения в контуре равна сумме ЭДС:
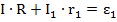
Для левой части уравнения 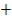 ставится, если направление обхода совпадает с направлением тока,
ставится, если направление обхода совпадает с направлением тока, 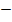 – если нет. Для правой
– если нет. Для правой 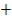 , если обход совершается от отрицательного полюса источника к положительному.
, если обход совершается от отрицательного полюса источника к положительному.
Второе правило запишем и для контура с сопротивлением R и источником 2:
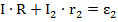
Теперь из уравнений, полученных путем записывания второго правила, выразим силы тока на каждом источнике:
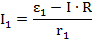
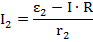
Теперь подставим полученные результаты в уравнение первого правила Кирхгофа
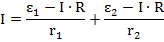
Полученное уравнение – линейное уравнение одной неизвестной:
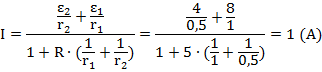
Ответ: