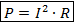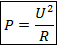Работа и мощность электрического тока

 1. Работа тока

Элек­три­че­ский ток, ко­неч­но же, не стал бы так ши­ро­ко ис­поль­зо­вать­ся, если бы не одно об­сто­я­тель­ство. Ра­бо­ту тока или же элек­тро­энер­гию легко пре­об­ра­зо­вы­вать в любую нуж­ную нам энер­гию или ра­бо­ту: теп­ло­вую, ме­ха­ни­че­скую, маг­нит­ную…

Для прак­ти­че­ско­го при­ме­не­ния тока пре­жде всего хо­чет­ся знать, какую ра­бо­ту можно об­ра­тить в свою поль­зу. Вы­ве­дем фор­му­лу для опре­де­ле­ния ра­бо­ты тока: 

Так как все ве­ли­чи­ны, вхо­дя­щие в фор­му­лу, можно из­ме­рить со­от­вет­ству­ю­щи­ми при­бо­ра­ми (ам­пер­метр, вольт­метр, часы), фор­му­ла яв­ля­ет­ся уни­вер­саль­ной.

Фор­му­лу можно также за­пи­сать в несколь­ко ином виде, ис­поль­зуя закон Ома:

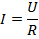
Если в ис­ход­ную фор­му­лу для ра­бо­ты тока под­ста­вить силу тока, за­пи­сан­ную таким об­ра­зом, то по­лу­чим:

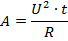
Если же из за­ко­на Ома вы­ра­зить на­пря­же­ние, то тогда:

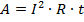
Ис­поль­зо­ва­ние этих фор­мул удоб­но, когда в цепи при­сут­ству­ет ка­кое-то одно со­еди­не­ние: па­рал­лель­ное для пер­во­го слу­чая и по­сле­до­ва­тель­ное для вто­ро­го.

 2. Закон Джоуля-Ленца

Осо­бое вни­ма­ние сле­ду­ет уде­лить теп­ло­во­му дей­ствию тока. При про­хож­де­нии тока через про­вод­ник, про­вод­ник на­гре­ва­ет­ся. По­че­му это про­ис­хо­дит? Мы уже за­тра­ги­ва­ли мо­ле­ку­ляр­ное стро­е­ние про­вод­ни­ков в теме о со­про­тив­ле­нии и от­ме­ча­ли, что при про­те­ка­нии тока сво­бод­ные элек­тро­ны стал­ки­ва­ют­ся с уз­ла­ми кри­стал­ли­че­ской ре­шет­ки. При этих столк­но­ве­ни­ях элек­тро­ны по­сто­ян­но при­да­ют неко­то­рую ско­рость узлам ре­шет­ки (рис. 1).

Рис. 1. Вза­и­мо­дей­ствие элек­тро­нов с уз­ла­ми кри­стал­ли­че­ской ре­шет­ки

Так как тем­пе­ра­ту­ра – мера теп­ло­во­го дви­же­ния, в про­цес­се «рас­тал­ки­ва­ния» тем­пе­ра­ту­ра про­вод­ни­ка по­вы­ша­ет­ся. В ка­кой-то мо­мент на­сту­па­ет рав­но­ве­сие, когда ко­ли­че­ство энер­гии, по­лу­ча­е­мое про­вод­ни­ком вслед­ствие про­хож­де­ния тока, равно ко­ли­че­ству энер­гии, ко­то­рое он от­да­ет в окру­жа­ю­щую среду.

В том слу­чае, когда ра­бо­та тока не пре­об­ра­зу­ет­ся в ме­ха­ни­че­скую или же ток не имеет хи­ми­че­ско­го дей­ствия, ра­бо­та тока эк­ви­ва­лент­на ко­ли­че­ству теп­ло­ты, вы­сво­бож­да­ю­ще­го­ся в окру­жа­ю­щую среду.

Фор­му­лу про­сче­та этого ко­ли­че­ства теп­ло­ты впер­вые неза­ви­си­мо друг от друга от­кры­ли двое уче­ных: рус­ский Эмиль Ленц и ан­гли­ча­нин Джеймс Джо­уль (рис. 2).

Закон Джо­у­ля-Лен­ца:

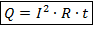
Как видно, пра­вая часть фор­му­лы в точ­но­сти по­вто­ря­ет одну из форм фор­му­лы для ра­бо­ты элек­три­че­ско­го тока.

Все­гда сле­ду­ет пом­нить, что в слу­чае, когда есть ка­кое-ли­бо дру­гое пре­об­ра­зо­ва­ние энер­гии тока, фор­му­ла Джо­у­ля-Лен­ца не вы­пол­ня­ет­ся.

Рис. 2. Джеймс Джо­уль и Эмиль Ленц со­от­вет­ствен­но

 3. Мощность тока

На­ря­ду с ра­бо­той тока очень важно от­ме­тить мощ­ность тока, так как эта ха­рак­те­ри­сти­ка яв­ля­ет­ся клю­че­вой в бы­то­вом ис­поль­зо­ва­нии элек­тро­энер­гии (на всех бы­то­вых при­бо­рах ука­за­но при­ем­ле­мое на­пря­же­ние его мощ­ность).

Опре­де­ле­ние. Мощ­ность – это ра­бо­та, вы­пол­нен­ная за еди­ни­цу вре­ме­ни (ско­рость вы­пол­не­ния током ра­бо­ты):

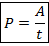
Еди­ни­ца из­ме­ре­ния мощ­но­сти – ватт:

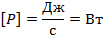
И те­перь, ис­поль­зуя наши зна­ния о ра­бо­те тока, мы без труда най­дем фор­му­лу для мощ­но­сти тока:

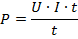
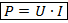
Или же, если ис­поль­зо­вать дру­гие виды фор­му­лы для ра­бо­ты: