Условная вероятность случайной величины

    Пример. Игральная кость подбрасывается один раз. Известно, что выпало более трёх очков. Какова вероятность того, что выпало чётное число очков?

    Зная, что выпало более трёх очков, мы можем сузить множество всех возможных элементарных исходов до трёх одинаково вероятных исходов: Ω = {4, 5, 6}, из которых событию A = {выпало четное число очков} благоприятствуют ровно два: А = {4, 6}. Поэтому Р(А) = 2/3.

    Посмотрим на вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: Ω = {1, 2, 3, 4, 5, 6}. Слова «известно, что выпало более трёх очков» означают, что в эксперименте произошло событие В = {4, 5, 6}. Слова «какова при этом вероятность того, что выпало чётное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении В происходит и А. Вероятность события А, вычисленную в предположении, что о результате эксперимента уже что-то известно (событие В произошло), мы будем обозначать через Р(А|В).

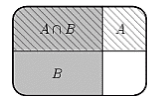
    Мы хотим найти, какую часть составляют исходы, благоприятствующие А внутри В (т.е. одновременно А и В), среди исходов, благоприятствующих В.

.

Мы пришли к выражению, которое можно считать определением условной вероятности.

Определение. 

Условной вероятностью события А при условии, что произошло событие В, называется число

Условная вероятность определена только в случае, когда P(B)>0.

Это определение бывает полезно использовать не для вычисления условной вероятности, а для последовательного вычисления вероятности нескольким событиям случиться одновременно, если известны соответствующие условные вероятности. А именно, справедливы следующие «теоремы умножения вероятностей».

Теорема 1. 

Если P(B)>0 и P(A)>0, то P(A∩B) = P(B)P(A|B) = P(A)P(B|A). 

Теорема 2. 

Для любых событий  A₁, . . . ,A_n верно равенство:

P(A₁, . . . ,A_n) = P(A₁)P(A₂|A₁)P(A₃|A₁A₂) * . . . * P(A_n|A₁ . . . A_n-1),

если все участвующие в нём условные вероятности определены.