Степенная функция и ее свойства и графики
Определение. Функция, заданная формулой f(x) = xn, где , называется степенной функцией с натуральным показателем.
Свойства функции f(x) = xn, где .
- D(f) = R;
- f(0) = 0; f(1) = 1. n = 2k,
. f(x) = x2k
- f(x) > 0
- 5) Функция четная, так как D(f) симметрична относительно 0x и f(-x) = (-x)2k = x2k = f(x).
- Функция возрастает на
; функция убывает на
,так как она четная.
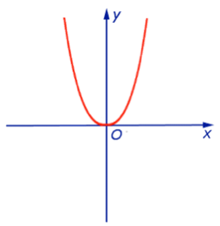
Следовательно, график функции аналогичен графику f(x) = x2
- D(f) = R;
- f(0) = 0; f(1) = 1. n = 2k - 1,
. f(x) = x2k - 1
- при x > 0 f(x) > 0; при x < 0 f(x) < 0
- E(f) = R
- Функция нечетная, так как D(f) симметрична относительно О(0;0) и f(-x) = (-x)2k - 1 = -x2k - 1 = -f(x).
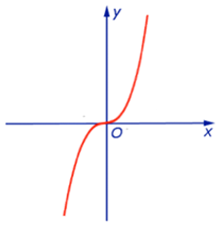
- Функция возрастает на R, так как если x2 > x1 , x22k - 1 > x12k - 1 и функция является нечетной, график функции аналогичен графику f(x) = x3 (кубическая парабола)
Графики степенных функций
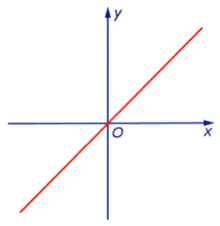
y = x

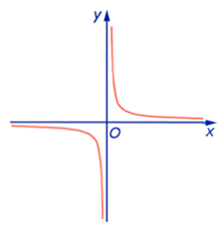
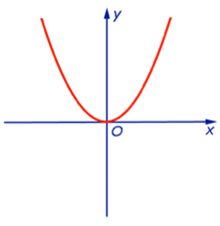
y = x2

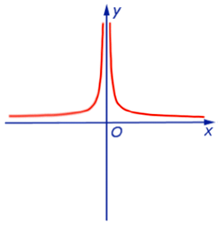
y = x3

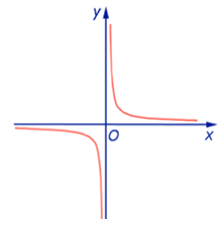
y = x4

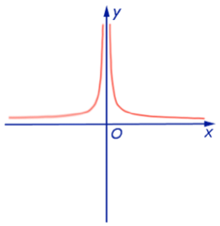
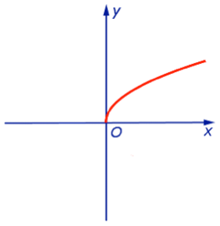
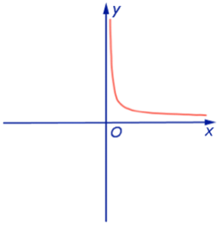
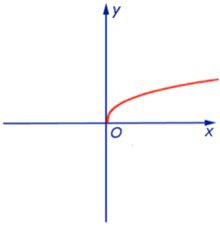
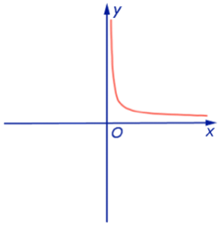
Вопросы к конспектам
Найдите область определения функции y = (x - x2)-1,5
Найдите область определения функции format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'math19290e2477baefb8e9b15f4a12a'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMi7iBBMAAADMAAAATmNtYXDEvmKUAAABHAAAAERjdnQgDVUNBwAAAWAAAAA6Z2x5ZoPi2VsAAAGcAAABdWhlYWQQC2qxAAADFAAAADZoaGVhCGsXSAAAA0wAAAAkaG10eE2rRkcAAANwAAAAEGxvY2EAHTwYAAADgAAAABRtYXhwBT0FPgAAA5QAAAAgbmFtZaBxlY4AAAO0AAABn3Bvc3QB9wD6AAAFVAAAACBwcmVwa1uragAABXQAAAAUAAADSwGQAAUAAAQABAAAAAAABAAEAAAAAAAAAQEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAg1UADev96AAAD6ACWAAAAAAACAAEAAQAAABQAAwABAAAAFAAEADAAAAAIAAgAAgAAACsAPSIS%2F%2F8AAAArAD0iEv%2F%2F%2F9b%2Fxd3xAAEAAAAAAAAAAAAAAVQDLACAAQAAVgAqAlgCHgEOASwCLABaAYACgACgANQAgAAAAAAAAAArAFUAgACrANUBAAErAAcAAAACAFUAAAMAA6sAAwAHAAAzESERJSERIVUCq%2F2rAgD%2BAAOr%2FFVVAwAAAQCAAFUC1QKrAAsASQEYsgwBARQTELEAA%2FaxAQT1sAo8sQMF9bAIPLEFBPWwBjyxDQPmALEAABMQsQEG5LEBARMQsAU8sQME5bELBfWwBzyxCQTlMTATIREzESEVIREjESGAAQBVAQD%2FAFX%2FAAGrAQD%2FAFb%2FAAEAAAIAgADrAtUCFQADAAcAZRgBsAgQsAbUsAYQsAXUsAgQsAHUsAEQsADUsAYQsAc8sAUQsAQ8sAEQsAI8sAAQsAM8ALAIELAG1LAGELAH1LAHELAB1LABELAC1LAGELAFPLAHELAEPLABELAAPLACELADPDEwEyE1IR0BITWAAlX9qwJVAcBV1VVVAAEAgAFVAtUBqwADADAYAbAEELEAA%2FawAzyxAgf1sAE8sQUD5gCxAAATELEABuWxAAETELABPLEDBfWwAjwTIRUhgAJV%2FasBq1YAAAAAAQAAAAEAANV4zkFfDzz1AAMEAP%2F%2F%2F%2F%2FWOhNz%2F%2F%2F%2F%2F9Y6E3MAAP8gBIADqwAAAAoAAgABAAAAAAABAAAD6P9qAAAXcAAA%2F7YEgAABAAAAAAAAAAAAAAAAAAAABANSAFUDVgCAA1YAgANWAIAAAAAAAAAAKAAAAKEAAAErAAABdQABAAAABABeAAUAAAAAAAIAgAQAAAAAAAQAAN4AAAAAAAAAFQECAAAAAAAAAAEAEgAAAAAAAAAAAAIADgASAAAAAAAAAAMAMAAgAAAAAAAAAAQAEgBQAAAAAAAAAAUAFgBiAAAAAAAAAAYACQB4AAAAAAAAAAgAHACBAAEAAAAAAAEAEgAAAAEAAAAAAAIADgASAAEAAAAAAAMAMAAgAAEAAAAAAAQAEgBQAAEAAAAAAAUAFgBiAAEAAAAAAAYACQB4AAEAAAAAAAgAHACBAAMAAQQJAAEAEgAAAAMAAQQJAAIADgASAAMAAQQJAAMAMAAgAAMAAQQJAAQAEgBQAAMAAQQJAAUAFgBiAAMAAQQJAAYACQB4AAMAAQQJAAgAHACBAE0AYQB0AGgAIABGAG8AbgB0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAATQBhAHQAaAAgAEYAbwBuAHQATQBhAHQAaAAgAEYAbwBuAHQAVgBlAHIAcwBpAG8AbgAgADEALgAwTWF0aF9Gb250AE0AYQB0AGgAcwAgAEYAbwByACAATQBvAHIAZQAAAwAAAAAAAAH0APoAAAAAAAAAAAAAAAAAAAAAAAAAALkHEQAAjYUYALIAAAAVFBOxAAE%2F)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%40font-face%7Bfont-family%3A'round_brackets18549f92a457f2409'%3Bsrc%3Aurl(data%3Afont%2Ftruetype%3Bcharset%3Dutf-8%3Bbase64%2CAAEAAAAMAIAAAwBAT1MvMjwHLFQAAADMAAAATmNtYXDf7xCrAAABHAAAADxjdnQgBAkDLgAAAVgAAAASZ2x5ZmAOz2cAAAFsAAABJGhlYWQOKih8AAACkAAAADZoaGVhCvgVwgAAAsgAAAAkaG10eCA6AAIAAALsAAAADGxvY2EAAARLAAAC%2BAAAABBtYXhwBIgEWQAAAwgAAAAgbmFtZXHR30MAAAMoAAACOXBvc3QDogHPAAAFZAAAACBwcmVwupWEAAAABYQAAAAHAAAGcgGQAAUAAAgACAAAAAAACAAIAAAAAAAAAQIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAgICAAAAAo8AMGe%2F57AAAHPgGyAAAAAAACAAEAAQAAABQAAwABAAAAFAAEACgAAAAGAAQAAQACACgAKf%2F%2FAAAAKAAp%2F%2F%2F%2F2f%2FZAAEAAAAAAAAAAAFUAFYBAAAsAKgDgAAyAAcAAAACAAAAKgDVA1UAAwAHAAA1MxEjEyMRM9XVq4CAKgMr%2FQAC1QABAAD%2B0AIgBtAACQBNGAGwChCwA9SwAxCwAtSwChCwBdSwBRCwANSwAxCwBzywAhCwCDwAsAoQsAPUsAMQsAfUsAoQsAXUsAoQsADUsAMQsAI8sAcQsAg8MTAREAEzABEQASMAAZCQ%2FnABkJD%2BcALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAA%2FtACIAbQAAkATRgBsAoQsAPUsAMQsALUsAoQsAXUsAUQsADUsAMQsAc8sAIQsAg8ALAKELAD1LADELAH1LAKELAF1LAKELAA1LADELACPLAHELAIPDEwARABIwAREAEzAAIg%2FnCQAZD%2BcJABkALQ%2FZD%2BcAGQAnACcAGQ%2FnAAAQAAAAEAAPW2NYFfDzz1AAMIAP%2F%2F%2F%2F%2FVre7u%2F%2F%2F%2F%2F9Wt7u4AAP7QA7cG0AAAAAoAAgABAAAAAAABAAAHPv5OAAAXcAAA%2F%2F4DtwABAAAAAAAAAAAAAAAAAAAAAwDVAAACIAAAAiAAAAAAAAAAAAAkAAAAowAAASQAAQAAAAMACgACAAAAAAACAIAEAAAAAAAEAABNAAAAAAAAABUBAgAAAAAAAAABAD4AAAAAAAAAAAACAA4APgAAAAAAAAADAFwATAAAAAAAAAAEAD4AqAAAAAAAAAAFABYA5gAAAAAAAAAGAB8A%2FAAAAAAAAAAIABwBGwABAAAAAAABAD4AAAABAAAAAAACAA4APgABAAAAAAADAFwATAABAAAAAAAEAD4AqAABAAAAAAAFABYA5gABAAAAAAAGAB8A%2FAABAAAAAAAIABwBGwADAAEECQABAD4AAAADAAEECQACAA4APgADAAEECQADAFwATAADAAEECQAEAD4AqAADAAEECQAFABYA5gADAAEECQAGAB8A%2FAADAAEECQAIABwBGwBSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFIAZQBnAHUAbABhAHIATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlACAAUgBvAHUAbgBkACAAYgByAGEAYwBrAGUAdABzACAAdwBpAHQAaAAgAGEAcwBjAGUAbgB0ACAAMQA4ADUANABSAG8AdQBuAGQAIABiAHIAYQBjAGsAZQB0AHMAIAB3AGkAdABoACAAYQBzAGMAZQBuAHQAIAAxADgANQA0AFYAZQByAHMAaQBvAG4AIAAyAC4AMFJvdW5kX2JyYWNrZXRzX3dpdGhfYXNjZW50XzE4NTQATQBhAHQAaABzACAARgBvAHIAIABNAG8AcgBlAAAAAAMAAAAAAAADnwHPAAAAAAAAAAAAAAAAAAAAAAAAAAC5B%2F8AAY2FAA%3D%3D)format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22aec8956637a99787bd197eacd77acce%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%222.5%22%20y%3D%2221%22%3Ef%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%228.5%22%20y%3D%2221%22%3E(%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22round_brackets18549f92a457f2409%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2218.5%22%20y%3D%2221%22%3E)%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2213.5%22%20y%3D%2221%22%3Ex%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22math19290e2477baefb8e9b15f4a12a%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2227.5%22%20y%3D%2221%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%23B94A48%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2234.5%22%20x2%3D%2268.5%22%20y1%3D%2216.5%22%20y2%3D%2216.5%22%2F%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2242.5%22%20y%3D%2212%22%3Ex%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22math19290e2477baefb8e9b15f4a12a%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2252.5%22%20y%3D%2212%22%3E%2B%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2261.5%22%20y%3D%2212%22%3E2%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2239.5%22%20y%3D%2230%22%3Ex%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22Arial%22%20font-size%3D%229%22%20text-anchor%3D%22middle%22%20x%3D%2245.5%22%20y%3D%2225%22%3E2%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22math19290e2477baefb8e9b15f4a12a%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2254.5%22%20y%3D%2230%22%3E%26%23x2212%3B%3C%2Ftext%3E%3Ctext%20fill%3D%22%23B94A48%22%20font-family%3D%22Arial%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2263.5%22%20y%3D%2230%22%3E3%3C%2Ftext%3E%3C%2Fsvg%3E)
Последнее изменение: Среда, 1 Февраль 2017, 19:02
