Перпендикуляр и наклонная. Расстояние от прямой до плоскости

Перпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.  Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной. 

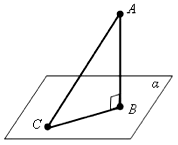
AB – перпендикуляр к плоскости α.  AC – наклонная, CB – проекция.  С – основание наклонной, B - основание перпендикуляра.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Расстояние от точки до плоскости, есть перпендикуляр, опущенный на эту плоскость, то есть расстояние от точки А до плоскости a, есть длина перпендикуляра АВ

Замечания.

1. Если прямая параллельна плоскости, то расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
2. Если две плоскости параллельны, то расстояние от произвольной точки одной из плоскостей до другой называется расстоянием между данными плоскостями.
3. Если две прямые скрещиваются, то расстояние между одной из этих прямых и плоскостью, проведённой через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

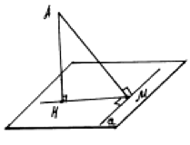
Теорема о трёх перпендикулярах. Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции, перпендикулярна и к самой наклонной.

Обратная теорема. Прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции

Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если точка лежит в плоскости. Проекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Расстояние от точки до плоскости, есть перпендикуляр, опущенный на эту плоскость, то есть расстояние от точки А до плоскости a, есть длина перпендикуляра АВ

Примечания:

1. Если прямая параллельна плоскости, то расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
2. Если две плоскости параллельны, то расстояние от произвольной точки одной из плоскостей до другой называется расстоянием между данными плоскостями.
3. Если две прямые скрещиваются, то расстояние между одной из этих прямых и плоскостью, проведённой через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

Если положение точки задано ее трехмерными координатами, а положение плоскости – линейным уравнением, то, чтобы найти расстояние от плоскости до точки, воспользуйтесь методами аналитической геометрии: • обозначьте координаты точки через x, y, z, соответственно (х – абсцисса, y – ордината, z – аппликата); • обозначьте через А, В, С, D параметры уравнения плоскости (А – параметр при абсциссе, В – при ординате, С – при аппликате, D – свободный член); • вычислите расстояние от точки до плоскости по формуле: 

где d – расстояние  между точкой и плоскостью, || - обозначение абсолютного значения (или модуля) числа.

Пример. 

Найдите расстояние между точкой М с координатами (2, 3, -1) и плоскостью, заданной уравнением: 7х-6у-6z+20=0. 

Решение. 

Из условий задачи следует, что: Мх=2, Му=3, Мz=-1, A=7, B=-6, C=-6, D=20. Подставьте эти значения в вышеприведенную формулу. Получится: 

Ответ: Расстояние от точки до плоскости равно 2 (условным единицам).

Вопросы к конспектам

Расстояние от некоторой точки до плоскости прямоугольника равно  см, а до всех его вершин - 3 см. Найдите диагональ прямоугольника.