Вписанные и описанные окружности

Определение 1. Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника .

В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником.

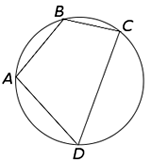
Теорема 1. Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.

Теорема 2. (Обратная  к теореме 1). Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d  –  длины сторон четырёхугольника, а p  – полупериметр, т.е.

Теорема Птолемея. Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

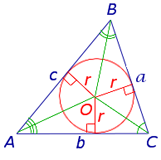
a, b, c – стороны треугольника, S –площадь,  r –  радиус вписанной окружности, p – полупериметр

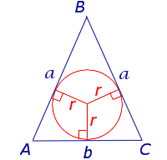
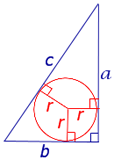
a – боковая сторона равнобедренного треугольника, b – основание,  r –  радиус вписанной окружности 

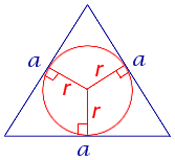
a – сторона равностороннего треугольника,  r  –  радиус вписанной окружности 

Для любого треугольника справедливо равенство:

S = 2R² sin A sin B sin C ,

где A, B, С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности

 Для любого треугольника справедливо равенство: , где a, b, c  – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Вопросы к конспектам

В четырехугольнике ABCD, вписанном в круг ABD = 50°, ADC = 82°. Найдите В четырехугольника.