Теорема Пифагора
Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство:
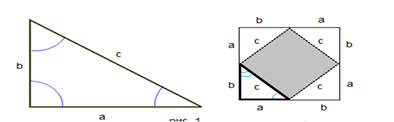
Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой c Докажем, что c2 = a2+ b2.
Достроим треугольник до квадрата со стороной a + b. Площадь S этого квадрата равна (a + b)2. C другой стороны, этот квадрат составлено из четырех равных прямоугольных треугольников, площадь каждого из которых равна ab, и квадрата со стороной c, поэтому
Таким образом,
(a + b)2 = 2ab + с2, откуда с2 = a2 + b2. Теорема доказана.
Вопросы к конспектам
Диагонали ромба 8см и 6см. Найдите стороны ромба.
Площадь равнобедренного прямоугольного треугольника равна 49. Найдите гипотенузу.
Последнее изменение: Воскресенье, 29 Январь 2017, 20:25
