Следствие из постулатов теории относительности
Введение
Постулаты СТО.
1. Все процессы в природе протекают одинаково во всех инерциальных системах отсчета (принцип относительности).
2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета, она не зависит ни от скорости источника, ни от скорости приемника светового сигнала.
Относительность расстояния
Оказывается, что расстояние не является абсолютной величиной, а зависит от скорости движения объекта относительно выбранной системы отсчета (Рис. 1.).
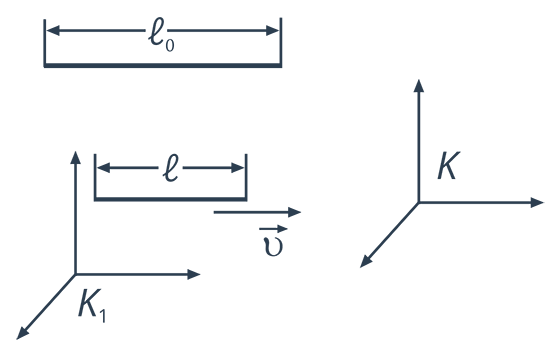
Рис. 1. Следствие 1
Пусть у нас есть стержень длиной 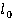 в системе отсчета
в системе отсчета 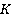 , относительно которой этот стержень покоится. Тогда длина
, относительно которой этот стержень покоится. Тогда длина 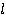 , этого стержня в системе отсчета
, этого стержня в системе отсчета 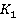 , относительно которой стержень движется со скоростью
, относительно которой стержень движется со скоростью 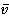 , определяется формулой:
, определяется формулой:
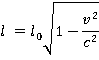
Получается, что длина стержня 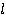 будет меньше ее первоначальной длины, если эта ручка будет двигаться со скоростью
будет меньше ее первоначальной длины, если эта ручка будет двигаться со скоростью 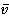 . В этом и состоит релятивистское сокращение длины.
. В этом и состоит релятивистское сокращение длины.
В повседневной жизни мы сталкиваемся с относительно небольшими скоростями и поэтому наблюдать релятивистское сокращение длины не можем.
Относительность промежутков времени
Оказывается, в зависимости от выбора системы отсчета и от того, с какой скоростью одна система отсчета движется относительно другой, будет зависеть и тот промежуток времени, который будет фиксироваться в той или иной системе.
Пусть интервал времени между двумя событиями, происходящими в одной и той же точке инерциальной системы 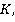 равен
равен 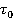 (Рис. 2.).
(Рис. 2.).
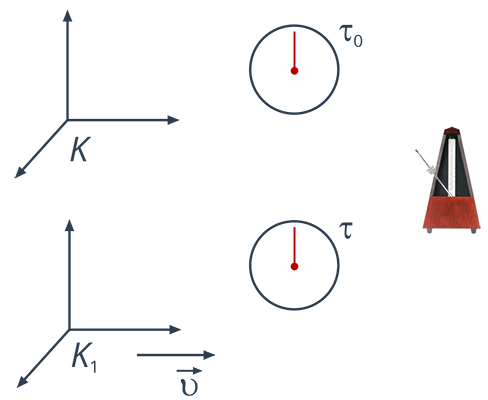
Рис. 2. Следствие 2
Например, этими событиями могут быть два удара метронома, отсчитывающего секунды, тогда интервал 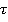 между этими событиями в системе отсчета
между этими событиями в системе отсчета 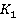 , которая движется относительно системы
, которая движется относительно системы 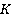 , со скоростью
, со скоростью 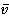 , выражается формулой:
, выражается формулой:
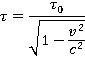
Очевидно, что 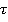 будет больше чем
будет больше чем 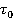 , в этом и состоит релятивистское замедление времени в движущейся системе отсчета.
, в этом и состоит релятивистское замедление времени в движущейся системе отсчета.
Релятивистский закон сложения скоростей
Для начала вспомним, каким был закон сложения скоростей в классической механике. Если, например, едет автомобиль со скоростью 20 км/час, а в этом авто летит муха со скоростью 5 км/час, то для наблюдателя на земле скорость мухи будет казаться 25 км/час.
Теперь рассмотрим сложение скоростей с точки зрения теории относительности.
Парадокс близнецов
Рассмотрим интересное следствие из релятивистского замедления времени (парадокс близнецов):
Представьте, что есть два брата-близнеца, Петр и Иван. Ваня – космонавт и отправляется в путешествие на ракете со скоростью, близкой к скорости света. Его нет приблизительно один год (по своему субъективному времени).
И, вернувшись на Землю, он встречается с братом, который, к его удивлению, выглядит намного старше него.
Рассмотрим это следствие на частном примере (Рис. 3.).
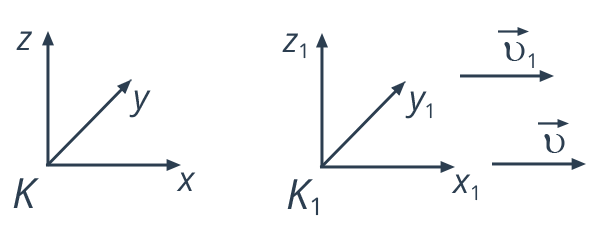
Рис. 3. Следствие 3
Пусть тело движется вдоль оси 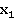 системы отсчета
системы отсчета 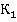 , которая, в свою очередь, движется со скоростью
, которая, в свою очередь, движется со скоростью 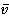 относительно системы отсчета
относительно системы отсчета 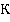 . Причем в процессе движения координатные оси
. Причем в процессе движения координатные оси 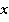 и
и 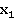 все время совпадают, а координатные оси
все время совпадают, а координатные оси 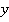 и
и 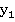 ,
, 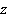 и
и 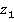 остаются параллельными.
остаются параллельными.
Обозначим скорость тела относительно 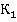 через скорость
через скорость 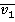 , а скорость этого же тела относительно
, а скорость этого же тела относительно 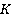 через
через 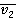 . Тогда релятивистский закон сложения скоростей будет иметь следующий вид:
. Тогда релятивистский закон сложения скоростей будет иметь следующий вид:
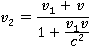
Связь между релятивистским и классическим законами сложения скоростей
Попробуем соотнести этот закон с эквивалентным ему в классической механике. Рассмотрим предельные случаи, когда скорости очень малы в сравнении со скоростью света.
Если скорость 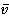 значительно меньше скорости света и скорость
значительно меньше скорости света и скорость 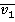 тоже значительно меньше скорости света, то частью знаменателя в формуле
тоже значительно меньше скорости света, то частью знаменателя в формуле 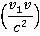 , можно пренебречь, и в таком случае мы получим классический закон сложения скоростей:
, можно пренебречь, и в таком случае мы получим классический закон сложения скоростей:
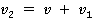
Рассмотрим еще один предельный случай. Представьте, что вы едете на поезде и включаете фонарик, для тех, кто стоит на земле, скорость света от фонарика останется 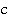 , а не
, а не 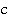 плюс скорость поезда, как могло показаться (случай, когда одна из скоростей равна скорости света).
плюс скорость поезда, как могло показаться (случай, когда одна из скоростей равна скорости света).
Тогда выходит, что 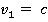 , подставим это значение в формулу, тогда:
, подставим это значение в формулу, тогда:
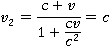
Выходит, что и скорость 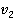 тоже будет равняться
тоже будет равняться 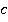 , как этого требует второй постулат теории относительности.
, как этого требует второй постулат теории относительности.
Релятивистский закон сложения скоростей справедлив, хотя и не совсем нагляден. Представьте себе наблюдателя на земле, он смотрит на большую ракету, которая движется относительно Земли со скоростью, близкой к скорости света. И от этой большой ракеты отделяется маленькая ракета, которая тоже начинает двигаться относительно большой со скоростью 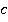 .
.
Из релятивистского закона сложения скоростей следует, что для наблюдателя на Земле и первая, и вторая ракеты будут двигаться со скоростями, близкими к скорости света 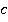 . Выходит, что фактически отличие в скоростях отсутствует. Хотя мы понимаем, что малая ракета движется с огромной скоростью относительно большой.
. Выходит, что фактически отличие в скоростях отсутствует. Хотя мы понимаем, что малая ракета движется с огромной скоростью относительно большой.
