Постулаты СТО

 Принцип относительности в классической механике

По­ло­же­ние о клас­си­че­ской ме­ха­ни­ке, той самой ме­ха­ни­ке, ко­то­рая, как ка­за­лось на конец XIX века, пол­но­стью опи­сы­ва­ет окру­жа­ю­щий нас мир, сфор­му­ли­ро­вал еще Исаак Нью­тон. Ос­нов­ные по­ло­же­ния клас­си­че­ской ме­ха­ни­ки:

- Дви­же­ние не ока­зы­ва­ет ни­ка­ко­го вли­я­ния на те­че­ние вре­ме­ни. Фи­зи­ки го­во­рят: время аб­со­лют­но. Ис­хо­дя из этого пред­по­ло­же­ния, мы по­лу­чи­ли клас­си­че­ские за­ко­ны сло­же­ния ско­ро­стей и пе­ре­ме­ще­ний при пе­ре­хо­де из одной си­сте­мы от­сче­та в дру­гую.

Пре­об­ра­зо­ва­ние Га­ли­лея:

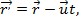
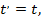
где: 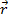 – ра­ди­ус-век­тор точки в пер­вой СО;

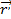  – ра­ди­ус-век­тор точки во вто­рой СО;

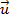  – ско­рость вто­рой СО от­но­си­тель­но пер­вой;

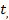  – время в пер­вой СО;

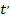  – время во вто­рой СО;

В клас­си­че­ской ме­ха­ни­ке пе­ре­ме­ще­ние и ско­рость от­но­си­тель­ны, а время аб­со­лют­но. Эти факты свя­за­ны с прин­ци­пом от­но­си­тель­но­сти Га­ли­лея, ко­то­рый фор­му­ли­ру­ет­ся так: всякое ме­ха­ни­че­ское яв­ле­ние при одних и тех же на­чаль­ных усло­ви­ях про­те­ка­ет оди­на­ко­во в любой инер­ци­аль­ной си­сте­ме от­сче­та.

Го­во­рят, что за­ко­ны клас­си­че­ской ме­ха­ни­ки ин­ва­ри­ант­ны от­но­си­тель­но пре­об­ра­зо­ва­ний Га­ли­лея, то есть при пе­ре­хо­де из одной инер­ци­аль­ной си­сте­мы от­сче­та в дру­гую инер­ци­аль­ную си­сте­му от­сче­та. Так об­сто­ит дело толь­ко в рам­ках клас­си­че­ской ме­ха­ни­ки. Про­ве­рим, будут ли эти пре­об­ра­зо­ва­ния ин­ва­ри­ан­ты и для дру­гих раз­де­лов фи­зи­ки.

 Противоречия

Пе­рей­дем к дру­гим об­ла­стям фи­зи­ки, может, в дру­гих ее раз­де­лах най­дут­ся такие яв­ле­ния, ход ко­то­рых будет су­ще­ствен­но раз­ным при пе­ре­хо­де из непо­движ­ной си­сте­мы от­сче­та в дви­жу­щу­ю­ся рав­но­мер­но и пря­мо­ли­ней­но. Тогда, со­по­ста­вив ход яв­ле­ний в непо­движ­ной и по­движ­ной си­сте­мах от­сче­та, мы смо­жем опре­де­лить ско­рость этих си­стем от­сче­та друг от­но­си­тель­но друга. С раз­ви­ти­ем элек­тро­ди­на­ми­ки ка­за­лось, что так оно и есть, дело в том, что урав­не­ния Макс­вел­ла, ко­то­рые лежат в ос­но­ве всей элек­тро­ди­на­ми­ки, в от­ли­чие от за­ко­нов Нью­то­на, как ока­за­лось, не ин­ва­ри­ант­ны при пе­ре­хо­де из одной си­сте­мы от­сче­та в дру­гую. Из урав­не­ний Макс­вел­ла сле­ду­ет один важ­ный факт: свет рас­про­стра­ня­ет­ся во всех на­прав­ле­ни­ях с одной и той же ско­ро­стью 300 000 км/с, при­чем эта ско­рость не за­ви­сит от того, дви­жет­ся ис­точ­ник света или по­ко­ит­ся. Фи­зи­ков того вре­ме­ни этот факт не удив­лял, им ка­за­лось, что свет пред­став­ля­ет собой ко­ле­ба­ния некой все­про­ни­ка­ю­щей среды, ко­то­рая на­хо­дит­ся во всех точ­ках Все­лен­ной и на­зы­ва­ет­ся эфи­ром. Это рас­про­стра­не­ние света в эфире и обу­слав­ли­ва­ют его по­сто­ян­ство.

Пред­ста­вим себе, что вы на­хо­ди­тесь в звез­до­ле­те, ко­то­рый мчит­ся в кос­ми­че­ском ва­ку­у­ме со ско­ро­стью 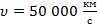 от­но­си­тель­но да­ле­ких звезд (рис. 1).

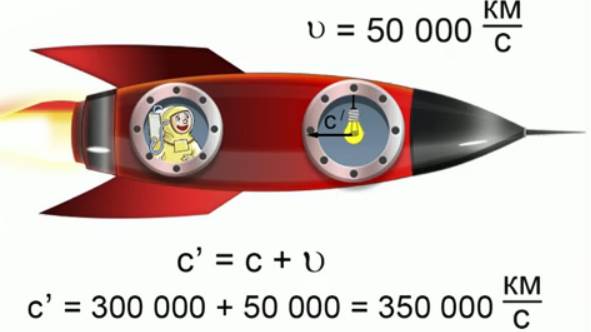
Рис. 1. При­мер со звез­до­ле­том

Вы си­ди­те лицом по ходу дви­же­нию звез­до­ле­та и смот­ри­те на лам­поч­ку, ко­то­рая на­хо­дит­ся в его но­со­вой части. Свет от лам­поч­ки, не об­ра­щая вни­ма­ния на ее дви­же­ние, пе­ре­ме­ща­ет­ся от­но­си­тель­но звезд со ско­ро­стью С = 300 000 км/с. Вы дви­же­тесь нав­стре­чу свету со ско­ро­стью 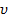, стало быть, от­но­си­тель­но вас свет дол­жен иметь ско­рость

 .

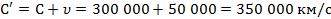Вы из­ме­ря­е­те эту ско­рость, со­по­став­ля­е­те ее с из­вест­ным зна­че­ни­ем С и при­хо­ди­те к вы­во­ду, что дви­га­е­тесь со ско­ро­стью 50 000 км/с, таким об­ра­зом, элек­тро­маг­нит­ные яв­ле­ния вроде бы поз­во­ля­ют от­ли­чить покой от рав­но­мер­но­го пря­мо­ли­ней­но­го дви­же­ния. То есть по­лу­ча­ет­ся па­ра­докс: с одной сто­ро­ны ско­рость света 300 000 км/с не долж­на за­ви­сеть от того, дви­жет­ся или по­ко­ит­ся ис­точ­ник света, с дру­гой сто­ро­ны, со­глас­но клас­си­че­ско­му за­ко­ну сло­же­ния ско­ро­стей, она долж­на за­ви­сеть от вы­бо­ра си­сте­мы от­сче­та.

Вы­хо­ды пред­ла­га­лись раз­ные, одно из мне­ний, сто­рон­ни­ком, ко­то­ро­го был Ло­ренц, гла­си­ло: инер­ци­аль­ные си­сте­мы от­сче­та, рав­но­прав­ные в ме­ха­ни­че­ских яв­ле­ни­ях, не яв­ля­ют­ся рав­но­прав­ны­ми в за­ко­нах элек­тро­ди­на­ми­ки.

То есть в элек­тро­ди­на­ми­ке су­ще­ству­ет некая при­ви­ле­ги­ро­ван­ная, глав­ная, аб­со­лют­ная си­сте­ма от­сче­та, ко­то­рую уче­ные свя­зы­ва­ли с так на­зы­ва­е­мым эфи­ром.

Про­ве­рить спра­вед­ли­вость на­ли­чия си­сте­мы от­сче­та, свя­зан­ной с эфи­ром, и на­ли­чие соб­ствен­но этого эфира по­пы­та­лись аме­ри­кан­ские уче­ные Май­кель­сон и Морли. Они про­ве­ря­ли, су­ще­ству­ет ли так на­зы­ва­е­мая аб­со­лют­ная си­сте­ма от­сче­та, свя­зан­ная с эфи­ром, и дви­жу­щи­е­ся от­но­си­тель­но нее все осталь­ные си­сте­мы от­сче­та, то есть так на­зы­ва­е­мый эфир­ный ветер, ко­то­рые могли вли­ять на ве­ли­чи­ну ско­ро­сти света. И, как вы толь­ко что убе­ди­лись, ни­ка­ко­го эфир­но­го ветра не су­ще­ству­ет. Фи­зи­ка того вре­ме­ни столк­ну­лась с нераз­ре­ши­мым па­ра­док­сом: что же спра­вед­ли­во – клас­си­че­ская ме­ха­ни­ка, элек­тро­ди­на­ми­ка Макс­вел­ла или что-то дру­гое.

 Постулаты СТО

На мо­мент пуб­ли­ка­ции своей ра­бо­ты Аль­берт Эйн­штейн не был при­знан­ным ми­ро­вым уче­ным, идеи, ко­то­рые он вы­ска­зал, ка­за­лись на­столь­ко ре­во­лю­ци­он­ны­ми, что в пер­вое время у них прак­ти­че­ски не было сто­рон­ни­ков. Тем не менее огром­ное ко­ли­че­ство экс­пе­ри­мен­тов и из­ме­ре­ний, ко­то­рые были про­ве­де­ны после этого, по­ка­за­ли спра­вед­ли­вость точки зре­ния Аль­бер­та Эйн­штей­на.

Сфор­му­ли­ру­ем еще раз про­бле­мы, с ко­то­ры­ми столк­ну­лась фи­зи­ка того вре­ме­ни и по­го­во­рим о тех ре­ше­ни­ях, ко­то­рые пред­ло­жил Эйн­штейн.

- Не уда­ет­ся об­на­ру­жить при­ви­ле­ги­ро­ван­ную си­сте­му от­сче­та, свя­зан­ную с непо­движ­ным ми­ро­вым эфи­ром.

Зна­чит, ее нет вовсе, нет этой при­ви­ле­ги­ро­ван­ной аб­со­лют­ной си­сте­мы от­сче­та? Аль­берт Эйн­штейн рас­ши­рил дей­ствие прин­ци­па Га­ли­лея в ме­ха­ни­ке на всю фи­зи­ку, и так по­лу­чил­ся прин­цип от­но­си­тель­но­сти от Эйн­штей­на: вся­кое фи­зи­че­ское яв­ле­ние при одних и тех же на­чаль­ных усло­ви­ях про­те­ка­ет оди­на­ко­во в любой инер­ци­аль­ной си­сте­ме от­сче­та.

То есть не вся­кое ме­ха­ни­че­ское яв­ле­ние, а любое фи­зи­че­ское яв­ле­ние.

Сле­ду­ю­щая труд­ность: элек­тро­ди­на­ми­ка про­ти­во­ре­чит ме­ха­ни­ке в том, что урав­не­ния Макс­вел­ла не ин­ва­ри­ант­ны от­но­си­тель­но пре­об­ра­зо­ва­ний Га­ли­лея, то есть это как раз та труд­ность, свя­зан­ная со ско­ро­стью света.

Может, Макс­велл неправ? Ни­че­го по­доб­но­го, элек­тро­ди­на­ми­ка Макс­вел­ла вполне спра­вед­ли­ва. Зна­чит, все осталь­ные об­ла­сти фи­зи­ки неспра­вед­ли­вы, невер­ны пре­об­ра­зо­ва­ния Га­ли­лея, ко­то­рые свя­зы­ва­ют эти части фи­зи­ки? Ведь из них вы­те­ка­ет клас­си­че­ский закон сло­же­ния ско­ро­стей, ко­то­рый мы ис­поль­зу­ем при ре­ше­нии задач, таких как: поезд едет со ско­ро­стью 40 км/ч, а пас­са­жир идет по ва­го­ну со ско­ро­стью 5 км/ч и от­но­си­тель­но на­блю­да­те­ля на земле, этот пас­са­жир будет дви­гать­ся со ско­ро­стью 45 км/ч (рис. 2).

Рис. 2. При­мер клас­си­че­ско­го сло­же­ния ско­ро­стей

Эйн­штейн фак­ти­че­ски за­яв­ля­ет: раз пре­об­ра­зо­ва­ния Га­ли­лея неспра­вед­ли­вы, то и этот закон сло­же­ния ско­ро­стей неспра­вед­лив. Пол­ный слом усто­ев, аб­со­лют­но оче­вид­ный жиз­нен­ный при­мер, аб­со­лют­но оче­вид­ный жиз­нен­ный закон ока­зы­ва­ет­ся неспра­вед­ли­вым, в чем же здесь про­бле­ма? Про­бле­ма глу­бо­ко внут­ри тех основ клас­си­че­ской ме­ха­ни­ки, ко­то­рые за­кла­ды­ва­лись еще Нью­то­ном. Ока­зы­ва­ет­ся, что глав­ная про­бле­ма клас­си­че­ской ме­ха­ни­ки со­сто­ит в том, что пред­по­ла­га­ет­ся, что все вза­и­мо­дей­ствия в рам­ках ме­ха­ни­ки рас­про­стра­ня­ют­ся мгно­вен­но. Рас­смот­рим, на­при­мер, гра­ви­та­ци­он­ное при­тя­же­ние тел.

Если сме­стить одно из тел в сто­ро­ну, то, со­глас­но за­ко­ну все­мир­но­го тя­го­те­ния, вто­рое тело по­чув­ству­ет этот факт мгно­вен­но, как толь­ко из­ме­нит­ся рас­сто­я­ние от него до пер­во­го тела, то есть вза­и­мо­дей­ствие пе­ре­да­ет­ся с бес­ко­неч­ной ско­ро­стью. В ре­аль­но­сти ме­ха­низм вза­и­мо­дей­ствия со­сто­ит в сле­ду­ю­щем: из­ме­не­ние по­ло­же­ния пер­во­го тела ме­ня­ет гра­ви­та­ци­он­ное поле во­круг него. Это из­ме­не­ние поля на­чи­на­ет бе­жать с ка­кой-то ско­ро­стью во все точки про­стран­ства, и, когда до­сти­га­ет точки, в ко­то­рой на­хо­дит­ся вто­рое тело, со­от­вет­ству­ю­щим об­ра­зом из­ме­ня­ет­ся и вза­и­мо­дей­ствие пер­во­го и вто­ро­го тел. То есть ско­рость рас­про­стра­не­ния вза­и­мо­дей­ствия об­ла­да­ет ка­кой-то ко­неч­ной ве­ли­чи­ной. Но если вза­и­мо­дей­ствия пе­ре­да­ют­ся с ка­кой-то ко­неч­ной ско­ро­стью, зна­чит, в при­ро­де долж­на су­ще­ство­вать ка­кая-то пре­дель­но до­пу­сти­мая ско­рость рас­про­стра­не­ния этих вза­и­мо­дей­ствий, мак­си­маль­ная ско­рость, с ко­то­рой вза­и­мо­дей­ствие может пе­ре­да­вать­ся. Об этом гла­сит вто­рой по­сту­лат, ко­то­рый от­во­дит ис­клю­чи­тель­ную роль ско­ро­сти света, прин­цип ин­ва­ри­ант­но­сти ско­ро­сти света: в каж­дой инер­ци­аль­ной си­сте­ме от­сче­та свет дви­жет­ся в ва­ку­у­ме с одной и той же ско­ро­стью. Ве­ли­чи­на этой ско­ро­сти не за­ви­сит от того, по­ко­ит­ся или дви­жет­ся ис­точ­ник света.

Таким об­ра­зом, опи­сан­ный выше при­мер с лам­поч­кой в звез­до­ле­те в ре­аль­но­сти нам про­ве­сти не удаст­ся, это будет про­ти­во­ре­чить этому по­сту­ла­ту тео­рии Эйн­штей­на. Ско­рость света от­но­си­тель­но на­блю­да­те­ля в звез­до­ле­те будет равна С, а не С +V, как мы го­во­ри­ли до этого, и на­блю­да­тель не смо­жет за­ме­тить факт дви­же­ния звез­до­ле­та. Клас­си­че­ский закон сло­же­ния ско­ро­стей при­ме­ни­тель­но ско­ро­сти света не ра­бо­та­ет, как это ни стран­но для нас, но ско­рость света для на­блю­да­те­ля на Земле и для кос­мо­нав­та будет со­вер­шен­но оди­на­ко­вой и рав­ной 300 000 км/с. Имен­но это по­ло­же­ние лежит в ос­но­ве тео­рии от­но­си­тель­но­сти и было вполне успеш­но до­ка­за­но огром­ным ко­ли­че­ством экс­пе­ри­мен­тов.

 Итоги

Ме­ха­ни­ка, ко­то­рая была по­стро­е­на на ос­но­ва­нии этих двух по­сту­ла­тов, носит на­зва­ние ре­ля­ти­вист­ской ме­ха­ни­ки (от ан­глий­ско­го relativity – «от­но­си­тель­ность»). Может по­ка­зать­ся, что ре­ля­ти­вист­ская ме­ха­ни­ка от­ме­ня­ет клас­си­че­скую ме­ха­ни­ку Нью­то­на, по­сколь­ку в ее ос­но­ве лежат дру­гие по­сту­ла­ты, но дело в том, что клас­си­че­ская ме­ха­ни­ка Нью­то­на – это част­ный слу­чай ре­ля­ти­вист­ской ме­ха­ни­ки Эйн­штей­на, ко­то­рый про­яв­ля­ет­ся при ско­ро­стях, зна­чи­тель­но мень­ших, чем ско­рость света. В окру­жа­ю­щем нас мире мы и живем в таких ско­ро­стях, ско­ро­сти, с ко­то­ры­ми мы стал­ки­ва­ем­ся, го­раз­до мень­ше ско­ро­сти света. По­это­му для опи­са­ния нашей жизни до­ста­точ­но клас­си­че­ской ме­ха­ни­ки Нью­то­на.

Для неболь­ших ско­ро­стей, зна­чи­тель­но мень­ших ско­ро­сти света, мы вполне успеш­но поль­зу­ем­ся клас­си­че­ской ме­ха­ни­кой, если же мы ра­бо­та­ем со ско­ро­стя­ми, близ­ки­ми к ско­ро­сти света, или хотим боль­шой точ­но­сти в опи­са­нии яв­ле­ний – мы долж­ны поль­зо­вать­ся спе­ци­аль­ной тео­ри­ей от­но­си­тель­но­сти, то есть ре­ля­ти­вист­ской ме­ха­ни­кой.