Опубликовано Kris Kim

Тесты с ответами и шпаргалки -> На русском языке -> Математика. ПГК, ЕНТ 2014 онлайн -> Равносторонний треугольник

от Kris Kim -
  • Все углы равны 600.
  • Каждая из высот является одновременно биссектрисой и медианой.
  • Центры описанной и вписанной окружностей совпадают.
  • Радиусы окружностей: r equals fraction numerator a square root of 3 over denominator 6 end fraction semicolon space space space R equals fraction numerator a square root of 3 over denominator 3 end fraction
  • Площадь: S equals fraction numerator a squared square root of 3 over denominator 4 end fraction

Тесты с ответами и шпаргалки -> На русском языке -> Математика. ПГК, ЕНТ 2014 онлайн -> Равнобедренный треугольник

от Kris Kim -

Треугольник, у которого две стороны равны.

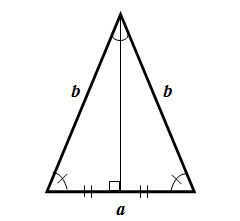
 Равнобедренный треугольник

  • Углы, при основании треугольника, равны
  • Высота, проведенная из вершины, является биссектрисой и медианой.

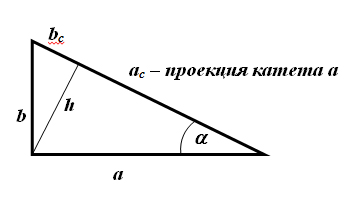
Тесты с ответами и шпаргалки -> На русском языке -> Математика. ПГК, ЕНТ 2014 онлайн -> Прямоугольный треугольник

от Kris Kim -

Прямоугольный треугольник

  • Теорема Пифагора: c2=a2+b2             Площадь: S equals 1 half a asterisk times b
  • Тригонометрические соотношения: cos alpha equals a over c semicolon space sin alpha equals b over c semicolon space t g alpha equals b over a
  • Центр описанной окружности лежит на середине гипотенузы.
  • Радиусы окружностей: r equals fraction numerator a plus b minus c over denominator 2 end fraction semicolon space R equals c over 2
  • Высота, опущенная на гипотенузу: h equals square root of a subscript c asterisk times b subscript c end root equals fraction numerator a asterisk times b over denominator c end fraction semicolon space open parentheses a over b close parentheses squared equals a subscript c over b subscript c
  • Катеты: a equals square root of a subscript c asterisk times c end root semicolon space space space b equals square root of b subscript c asterisk times c end root