Гомотетия. Подобные фигуры. Признаки подобия треугольников, подобие прямоугольных треугольников
Преобразование фигуры F в фигуру F' называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз, т.е. если произвольные точки А и В фигуры F при этом преобразовании переходят в точки A1 и В1 фигуры F1, то A1B1 = κAB, где κ>0. Число κ называется коэффициентом подобия (κ>0). При k=1 преобразование подобия является движением.
Частным случаем преобразования подобия является преобразование гомотетии.
Гомотетия с центром в точке O и коэффициентом k называется такое преобразование плоскости, при котором любая точка A переходит в точку A' такую, что (рис. а, б для κ > 0, κ < 0). В частности, при κ = -1, гомотетия представляет собой центральную симметрию.
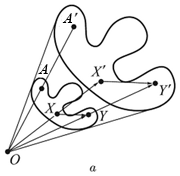
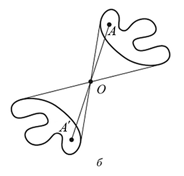
Основное свойство гомотетии:
При гомотетии с коэффициентом k отрезок AB переходит в отрезок A'B', параллельный AB и такой, что , а любая фигура F отображается в фигуру F', подобную F с коэффициентом подобия k. При этом всякий элемент фигуры F отображается в соответствующий элемент фигуры F'.
Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия. Для обозначения подобия фигур используется специальный значок: ~ Запись F~F' читается так: «Фигура F подобна фигуре F'».
Докажем, что если фигура F1 подобна фигуре F2, а фигура F2 подобна фигуре F3, то фигуры F1и F3 подобны.
Пусть Х1 и Y1 -- две произвольные точки фигуры F1. Преобразование подобия, переводящее фигуру F1 в F2, переводит эти точки в точки Х2, Y2, для которых X2Y2 = k1X1Y1.
Преобразование подобия, переводящее фигуру F2 в F3, переводит точки Х2, Y2 в точки Х3, Y3, для которых X3Y3 = - k2X2Y2.
Из равенств X2Y2= k1X1Y1, X3Y3 = k2X2Y2 следует, что X3Y3 - k1k2X1Y1. А это значит, что преобразование фигуры F1 в F3, получающееся при последовательном выполнении двух преобразований подобия, есть подобие. Следовательно, фигуры F1 и F3 подобны, что и требовалось доказать.
В записи подобия треугольников: DABC~DA1B1C1 - предполагается, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. А переходит в А1, В в B1 и С в С1.
Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, у подобных треугольников ABC и А1В1С1 ÐA=ÐА1, ÐВ=ÐВ1, ÐС=ÐС1
ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ
- Подобие по двум углам. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Подобие по двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
- Подобие по трем сторонам. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Признаки подобия прямоугольных треугольников
- Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
- Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
- Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
Следствие 1. Прямая, пересекающая треугольник и параллельная стороне треугольника, отсекает от этого треугольника подобный треугольник.
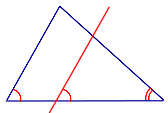
Следствие 2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия
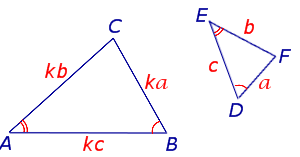
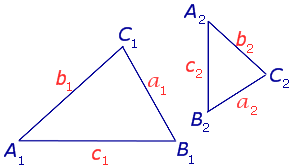
Определение 1. В треугольниках A1B1C1 и A2B2C2, вершины A1 и A2, B1 и B2, C1 и C2 называют сходственными вершинами,
стороны A1B1 и A2B2, A1C1 и A2C2, B1C1 и B2C2 называют сходственными сторонами,
углы A1 и A2, B1 и B2, C1 и C2 называют сходственными углами
Определение 2. Треугольники A1B1C1 и A2B2C2 называют подобными треугольниками, если их сходственные углы равны, а сходственные стороны пропорциональны.
Другими словами, треугольники A1B1C1 и A2B2C2 подобны, если, во-первых, A1 =
A2;
B1 =
B2;
C1 =
C2 а, во-вторых, существует положительное число k, такое, что справедливы равенства: a1 = ka2; b1 = kb2; c1 = kc2;
Определение 3. В случае, когда треугольники A1B1C1 и A2B2C2 подобны, число k, заданное формулами , называют коэффициентом подобия треугольников A1B1C1 и A2B2C2
Признаки подобия треугольников
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Вопросы к конспектам
