Взаимное расположение прямой и плоскости в пространстве. Признаки параллельности прямой и плоскости в пространстве

Все возможные случаи взаимного расположения прямой и плоскости в пространстве :

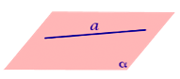
1. Прямая лежит на плоскости (принадлежит плоскости)

Прямая лежит на плоскости, если все точки прямой принадлежат плоскости.

Замечание. Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости.

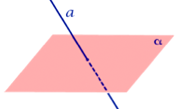
2.  Прямая пересекает плоскость

Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку

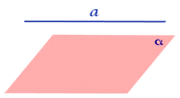
3. Прямая параллельна плоскости

Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются

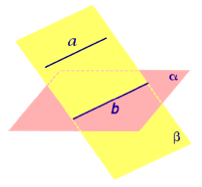
      Утверждение 1. Предположим, что прямая   a   и плоскость   α  параллельны, а плоскость   β   проходит через прямую   a . Тогда возможны два случая:

1. Плоскость   β   параллельна плоскости α;
2. Плоскость   β   пересекает плоскость α. В этом случае прямая b, которая является линией пересечения плоскостей α и β, будет параллельна прямой a. 
     

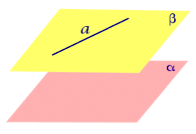
   Доказательство. Рассмотрим случай 2 и предположим противное. Предположим, что прямые   a   и   b   пересекаются в некоторой точке   P .

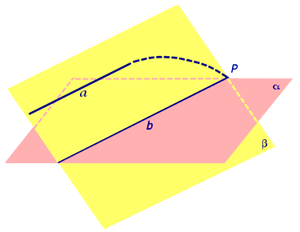
Но тогда точка   P   оказывается точкой пересечения прямой   a   и плоскости   α ,   и мы получаем противоречие с тем, что прямая   a   и плоскость  α  параллельны. Полученное противоречие и завершает доказательство утверждения 1.

      Утверждение 2  (признак параллельности прямой и плоскости). Если прямая   a ,   не лежащая в плоскости   α ,   параллельна некоторой прямой   b,   лежащей в плоскости   α ,   то прямая   a   и плоскость   α  параллельны.

      Доказательство. Докажем признак параллельности прямой и плоскости "от противного". Предположим, что прямая   a   пересекает плоскость  α  в некоторой точке   P . Проведем плоскость   β   через параллельные прямые a и b.

      Точка   P   лежит на прямой   a   и принадлежит плоскости   β.    Но по предположению точка   P   принадлежит и плоскости   α  , следовательно точка   P   лежит на прямой   b ,  по которой пересекаются плоскости   α  и   β .  Однако прямые     a   и   b   параллельны по условию и не могут иметь общих точек.

      Полученное противоречие завершает доказательство признака параллельности прямой и плоскости.

Теоремы

•  Если прямая, пересекающая плоскость, перпендикулярна двум прямым, лежащим в этой плоскости и проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
• Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
• Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
• Если прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.
• Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, расположенной в этой плоскости, то она параллельна этой плоскости.
• Если прямая параллельна плоскости, то она параллельна некоторой прямой на этой плоскости.
• Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
• Все точки прямой, параллельной плоскости, одинаково удалены от этой плоскости.