Площадь прямоугольника и квадрата

Площадь -это внутренняя часть любой геометрической фигуры, в простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.

Площадь фигуры определяется положительным числом.

Две фигуры называются равносоставленными, если, определённым образом разрезав одну из них на конечное число частей, можно (располагая эти части иначе) составить из них вторую фигуру.

Две равнососталенные фигуры равновелики, т.е. имеют одинаковую площадь. На этом основан простой способ вычисления площадей, называемый методом разложения (или разбиения). Метод этот (известный еще Евклиду, жившему свыше 2000 лет назад) заключается в следующем: для вычисления площади пытаются разбить фигуру на конечное число частей таким образом, чтобы из этих частей можно было составить более простую фигуру (площадь которой нам уже известна).

Итак, метод разбиения основан на том, что всякие два равносоставленных многоугольника равновелики.

Естественно поставить обратный вопрос: всякие ли два многоугольника, имеющих одинаковую площадь, равносоставлены? Ответ на этот вопрос был дан (почти одновременно) венгерским математиком Фаркашем Бойяи (1832г.) и немецким офицером и любителем математики Гервином (1833г.): два многоугольника, имеющих равные площади,равносоставленны.

Два равных многоугольника имеют одну и ту же площадь.

Многоугольник, составленный из нескольких многоугольников, имеет площадь, равную сумме их площадей.

За единицу площади принимается площадь квадрата со стороной, равной единице длины.

Итак, число называется площадью многоугольника, если оно удовлетворяет этим трём требованиям.

Аксиомы площади

 1. Равные фигуры имеют равные площади.

 2. Площадь некоторого квадрата, сторона которого является единицей длины, равна единице.

 3. Если фигура А разбита на две части В и С то S(А)=S(В)+S(С)

Площадь прямоугольника равна произведению его смежных сторон:

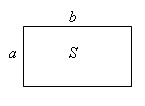
S = a × b

Для вычисления площади квадрата нужно умножить его длину на саму себя.

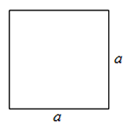
 S = a × a =  a²

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Площадь всей фигуры равна сумме площадей её частей.

Площадь произвольного четырехугольника ABCD равна половине произведения диагоналей и синуса угла между ними:

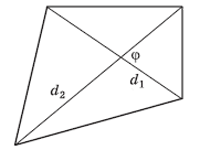 S = d₁d₂sina

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника