Системы линейных уравнений с двумя переменными

Найдем пары значений удовлетворяющие двум уравнения с двумя неизвестными одновременно, например: 2х+3у =1 и х-5у =0, то есть необходимо найти пересечение множеств решений этих уравнений. В таких случаях говорят, что надо решить систему уравнений 2х+3у =1 и х-5у =0.

Систему уравнений принято записывать с помощью фигурной скобки.

Например,

Пара значений переменных, обращающая в истинное равенство каждое уравнение системы, называется решением системы уравнений с двумя переменными.

Решить систему уравнений – значит найти множество её решений.
Рассмотрим системы двух линейных уравнений с двумя переменными, в которых в каждом уравнении хотя бы один из коэффициентов отличен от нуля.
Графическое решение систем такого вида сводится к отысканию координат общих точек двух прямых.
Как известно, две прямые на плоскости могут быть пересекающимися или параллельными. В случае параллельности прямые либо не имеют общих точек, либо совпадают.
Рассмотрим каждый из этих случаев.

Выразим переменную у через х:

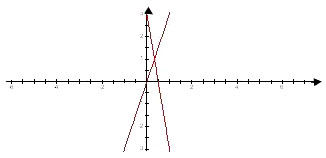
По графику можно определить координаты пересечения двух прямых: 

Если в каждом уравнении системы двух линейных уравнений с двумя переменными хотя бы один из коэффициентов при переменной не равен нулю, то система либо имеет единственное решение, либо имеет бесконечно много решений.

Существуют несколько способов решения систем уравнения:

1. Графический
2. Способ подстановки
3. Способ сложения

Алгоритм решения системы линейных уравнений способом подстановки:

1. 1. Выбрать одно уравнение (лучше выбирать то, где числа меньше) и выразить из него одну переменную через другую, например, x через y. (можно и y через x).
   2. Полученное выражение подставить вместо соответствующей переменной в другое уравнение. Таким образом, у нас получится линейное уравнение с одной неизвестной.
   3. Решаем полученное линейное уравнение и получаем решение.
   4. Подставляем полученное решение в выражение, полученное в первом пункте, получаем вторую неизвестную из решения.
   5. Выполнить проверку полученного решения.

Пример 1. Решить систему уравнений:

Решение:

Найдем значение х, подставив значение у в первое уравнение:

Проверка: 

Пример 2: Решим способом сложения следующую систему линейных уравнений с двумя неизвестными:

Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.

Получим следующую систему уравнений: из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.

Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.

Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.

Ответ: (6, 14)

Вопросы к конспектам

Решите систему уравнений: 

Решите систему уравнений: 

Решите систему уравнений: 

Решите систему уравнений: 

Решите систему уравнений: 

Решите систему уравнений: 

Найдите значение х: 

Решите систему уравнений: 

Решите систему уравнений: 

Решите систему уравнений: