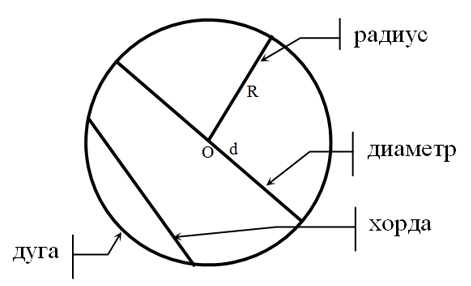
Длина окружности: 

Площадь круга: 

Стандартный вид:   317,3 = 3,173×10² ;          0,00003173 = 3,173×10^-5

Форма записи:          3173 = 3× 1000 + 1× 100 + 7× 10 + 3

Пусть n : m = k,  где n, m, k – натуральные числа.
Тогда m – делитель числа n, а n – кратно числу m.

Число n называется простым, если его делителями являются
только единица и само число n.

 Множество простых чисел:            {2; 3; 5; 7; 11; 13; . . .; 41; 43; 47 и т.д.}

 Числа n и m называются взаимно простыми, если у них нет общих делителей, кроме единицы.

Формула деления с остатком:       

n = m×k + r, 

где n – делимое, m - делитель, k - частное, r – остаток: 0 £ r < m

Пример:
Любое число можно представить в виде:
n = 2k + r, где r = {0; 1}
или n = 4k + r, где r = {0; 1; 2; 3}

Расстояние между точками: 

Координаты вектора:            

т. C - середина отрезка  AB:      

Уравнение окружности: