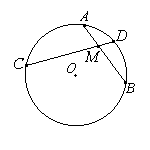
Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.

Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

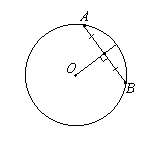
Дуги, заключенные между параллельными хордами, равны. В окружности равные хорды равноудалены от центра окружности.

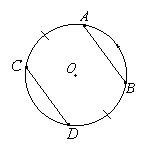
Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: 

Переменные x и y связаны обратно пропорциональной зависимостью  , где  , k - коэффициент обратной пропорциональности.

• Графиком обратной пропорциональности  является кривая, состоящая из двух ветвей, симметричных относительно начала координат. Этот график называется гиперболой.
• Область определения функции функции  есть множество всех чисел, отличных от нуля, т.е D(f)=(−;0)(0:+)
• Гипербола не имеет общих точек с осями координат, а лишь сколь угодно близко к ним приближается, т.к.  .
• Если k > 0 , то ветви гиперболы в I и III координатных четвертях, если k < 0, то ветви гиперболы расположены во II и IV четвертях координатной плоскости.

Функция модуль задается уравнением y = | x |.

График функция модуль состоит из биссектрис первого и второго координатных углов

Свойства:

Функция модуль является четной функцией.
Производная функции модуль в точке x=0 не существует.
График функции модуль симметричен относительно оси ординат.

Функция корень

Квадрат суммы (a + b)² = a² + 2ab + b²

Квадрат разности (a - b)² = a² - 2ab + b²

Разность квадратов a² – b² = (a + b)(a – b)

Куб суммы (a + b)³ = a³ + 3a²b + 3ab² +  b³

Куб разности (a - b)³ = a³ - 3a²b + 3ab² -  b³

Сумма кубов a³ + b³ = (a + b)( a² - ab + b²)

Разность кубов a³ – b³ = (a – b)( a² + ab + b²)