Решение квадратных неравенств с помощью графика

Квадратным неравенством называют неравенство вида ах² + bх + с> 0, где  (вместо знака > может быть, разумеется, любой другой знак неравенства).

Алгоритм решения квадратного неравенства ах² + bх + 0 > 0 (ах² + bх + с < 0)

1. Найти корни квадратного трехчлена
2. Отметить найденные корни на оси х и определить, куда (вверх или вниз) направлены ветви параболы, служащие графиком функции у= ах² + bх + с; сделать набросок графика.
3. С помощью полученной геометрической модели определить, на каких промежутках оси х ординаты графика положительны (отрицательны); включить эти промежутки в ответ. 

Пример 1. Решить неравенство:

а) х² - 2х - 3 >0;       б) х² - 2х - 3 < 0;

в) х² - 2х - 3 ≥ 0;       г) х² - 2х - 3 ≤ 0.

Решение:

а) Рассмотрим параболу у = х² - 2х - 3,

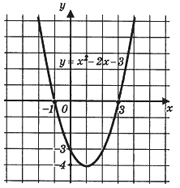
Решить неравенство х² - 2х - 3 > 0 — это значит ответить на вопрос, при каких значениях х ординаты точек параболы положительны.

Замечаем, что у > 0, т. е. график функции расположен выше оси х, при х < -1 или при

х > 3.

Значит, решениями неравенства служат все точки открытого луча  , а также все точки открытого луча .

Используя знак  (знак объединения множеств), ответ можно записать так: . Впрочем, ответ можно записать и так: х < - 1; х > 3.

б) Неравенство х² - 2х - 3 < 0, или у < 0, где у = х² - 2х - 3, также можно решить с помощью рис. 117: график расположен ниже оси х, если -1 < х < 3. Поэтому решениями данного неравенства служат все точки интервала (— 1, 3).

в) Неравенство х² - 2х - 3 ≥ 0 отличается от неравенства х² - 2х - 3 > 0 тем, что в ответ надо включить и корни уравнения х² - 2х - 3 = 0, т. е. точки х = -1

и х = 3. Таким образом, решениями данного нестрогого неравенства являются все точки луча  , а также все точки луча .

г) Неравенство х² - 2х - 3 ≤0 отличается от неравенства х² - 2х - 3 < 0 тем, что в ответ надо включить и корни уравнения х² - 2х - 3 = 0, т. е. х = -1 и х = 3. Следовательно, решениями данного нестрогого неравенства служат все точки отрезка [-1, 3].

Вопросы к конспектам

По графику функции у=х²-4х+3 определить промежутки, на которых функция принимает отрицательные значения.